
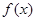 为定义在
为定义在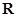 上的奇函数,当
上的奇函数,当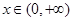 时,
时,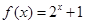 ,则当
,则当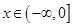 时,
时,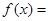 _______________.
_______________.科目:高中数学 来源:不详 题型:解答题
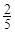 小时,种植一捆沙棘树苗用时
小时,种植一捆沙棘树苗用时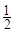 小时.应如何分配A,B两组的人数,使植树活动持续时间最短?
小时.应如何分配A,B两组的人数,使植树活动持续时间最短?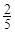 小时,而每名志愿者种植一捆沙棘树苗实际用时
小时,而每名志愿者种植一捆沙棘树苗实际用时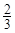 小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.
小时,于是从A组抽调6名志愿者加入B组继续种植,求植树活动所持续的时间.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?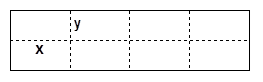
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
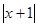 ,g(x)=2|x|+a.
,g(x)=2|x|+a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com