解:(1)由题意,总的基本事件数是6×6×6=216
长度为a,b,c的三条线段能构成直角三角形有下列几种情形,3,4,5;3,5,4;4,3,5;4,5,3;5,3,4;5,4,3.共六种
故长度为a,b,c的三条线段能构成直角三角形的概率为
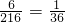
(2)连续抛掷三次,点数分别为a,b,c的基本事件总数为6×6×6=216
长度为a,b,c的三条线段能构成等腰三角形有下列几种情形
①当a=b=c时,能构成等边三角形,有1,1,1;2,2,2;…;6,6,6共6种可能.
②当a,b,c恰有两个相等时,设三边长为x,y,z,其中x∈{2,3,4,5,6}且x=z,且x≠y;
若x=2,则y只能是1或3,共有2种可能;若x=3,则y只以是1,2,4,5,共有4种可能;
若x=4,5,6,则y只以是集合{1,2,3,4,5,6}中除x外的任一个数,共有3×5种可能;
∴当a,b,c恰有两个相等时,符合要求的a,b,c共有3×(2+4+3×5)=63
故所求概率为
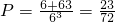
分析:(1)由题意,连续抛掷三次,先求出总的基本事件数216,求出可构成直角三角形的基本事件数.
(2)先求出总的基本事件数为216,再求出可构成等腰三角形的基本事件数.
点评:本题考查列举法计算基本事件数及事件发生的概率,列举时要注意不重不漏,分类列举.

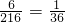


 一本好题口算题卡系列答案
一本好题口算题卡系列答案 如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点
如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点