Question

10．已知过抛物线y²=$\frac{16}{3}$x的焦点F的直线l交抛物线于A，B两点，交其准线于C点，已知$\overrightarrow{CB}$=3$\overrightarrow{BF}$，则线段AB的中点M到准线的距离为（　　）

• A． $\frac{8}{3}$
• B． 3
• C． $\frac{16}{3}$
• D． 6

Answer 1

分析 构造辅助线，由已知$\overrightarrow{CB}$=3$\overrightarrow{BF}$，及抛物线可知，求得丨BC丨及丨DC丨的关系，即可求得直线的倾角，由中位线定理及椭圆的性质，求得即丨MP丨=$\frac{1}{2}$丨AB丨，可求出线段AB的中点到抛物线准线的距离．

解答 解：抛物线y²=$\frac{16}{3}$x，焦点坐标为（$\frac{4}{3}$，0）
过点A、B和M分别做准线的垂线交准线于E、D和F点，
∵$\overrightarrow{CB}$=3$\overrightarrow{BF}$，
$\overrightarrow{CB}$=3$\overrightarrow{BF}$，且|BF|=|BD|，丨AE丨=丨AF丨，
设丨BF丨=丨BD丨=a，直线AB的倾角为α，
∴丨BC丨=3a，丨DC丨=2$\sqrt{2}$a，
sinα=sin∠DBC=$\frac{丨DC丨}{丨BC丨}$=$\frac{2\sqrt{2}}{3}$，
AB的斜率为-2$\sqrt{2}$，
直线AB的方程为：y=-2$\sqrt{2}$（x-$\frac{4}{3}$），
代入椭圆方程整理得：9x²-30+16=0，
x₁+x₂=$\frac{10}{3}$，
线段丨AB丨=p+x₁+x₂=6，
由中位线定理可知：线段AB的中点M到准线的距离为d=$\frac{1}{2}$丨AB丨=3，
故答案选：B．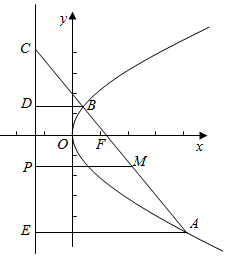

点评 本题考查解决抛物线上的点到焦点的距离问题，中位线定理，利用抛物线的定义将到焦点的距离转化为到准线的距离是关键，属于中档题．