
已知圆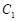 的参数方程为
的参数方程为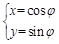 (
(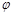 为参数),以坐标原点
为参数),以坐标原点 为极点,x轴的正半轴为极轴建立极坐标系,圆
为极点,x轴的正半轴为极轴建立极坐标系,圆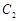 的极坐标方程为
的极坐标方程为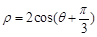 .
.
(Ⅰ)将圆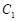 的参数方程化为普通方程,将圆
的参数方程化为普通方程,将圆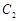 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)圆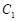 、
、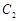 是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
是否相交,若相交,请求出公共弦的长;若不相交,请说明理由.
(Ⅰ)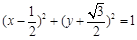 。(Ⅱ)
。(Ⅱ) 。
。
【解析】
试题分析:
思路分析:(Ⅰ)由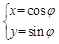 利用“平方关系”消参得到:x2+y2=1,
利用“平方关系”消参得到:x2+y2=1,
应用两角和的余弦公式变形,得到ρ=2cos(θ+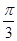 )=cosθ-
)=cosθ-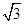 sinθ,
sinθ,
即ρ2=ρcosθ-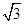 ρsinθ利用公式化为普通方程。
ρsinθ利用公式化为普通方程。
(Ⅱ)通过计算圆心距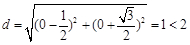 ,
,
判断两圆相交,通过建立方程组,进一步求弦长,也可考虑“几何法”。
解:(Ⅰ)由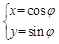 得x2+y2=1,
得x2+y2=1,
又∵ρ=2cos(θ+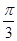 )=cosθ-
)=cosθ-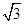 sinθ,
sinθ,
∴ρ2=ρcosθ-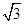 ρsinθ.∴x2+y2-x+
ρsinθ.∴x2+y2-x+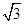 y=0,
y=0,
即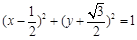 5分
5分
(Ⅱ)圆心距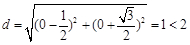 ,
,
得两圆相交,由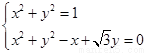
得,A(1,0),B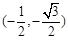 ,
,
∴  10分
10分
考点:极坐标方程、参数方程与普通方程的互化,参数方程的应用。
点评:中档题,参数方程化为普通方程,常用的“消参”方法有,代入消参、加减消参、平方关系消参等。利用参数方程,往往会将问题转化成三角函数问题,利用三角公式及三角函数的图象和性质,化难为易。极坐标方程化为普通方程,常用的公式有, ,
,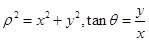 等。
等。


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二下期中理科数学试卷(解析版) 题型:填空题
已知圆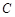 的参数方程为
的参数方程为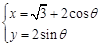 (
( 为参数),若
为参数),若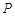 是圆
是圆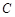 与
与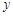 轴正半轴的交点,以坐标原点
轴正半轴的交点,以坐标原点 为极点,
为极点,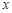 轴的正半轴为极轴建立极坐标系,则过点
轴的正半轴为极轴建立极坐标系,则过点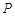 的圆
的圆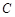 的切线的极坐标方程为
.
的切线的极坐标方程为
.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二第二学期月考文科数学试卷(解析版) 题型:解答题
已知圆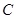 的参数方程为
的参数方程为 (
(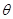 为参数),
为参数),
(1)以原点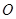 为极点、
为极点、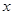 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆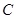 的极坐标方程;
的极坐标方程;
(2)已知直线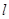 经过原点
经过原点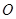 ,倾斜角
,倾斜角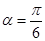 ,设
,设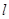 与圆
与圆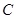 相交于
相交于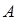 、
、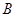 两点,求
两点,求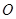 到
到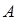 、
、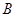 两点的距离之积。
两点的距离之积。
查看答案和解析>>
科目:高中数学 来源:2011年广东省东莞市教育局教研室高三上学期数学文卷 题型:填空题
(坐标系与参数方程选做题)
已知圆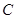 的参数方程为
的参数方程为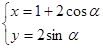 (
(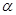 为参数).以原点为极点,
为参数).以原点为极点,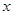 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线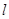 的极坐标方程为
的极坐标方程为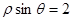 ,则直线
,则直线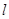 与圆
与圆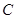 的交点的直角坐标为 .
的交点的直角坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com