
【题目】定义:若对定义域内任意x,都有![]() (a为正常数),则称函数
(a为正常数),则称函数![]() 为“a距”增函数.
为“a距”增函数.
(1)若![]() ,
,![]() (0,
(0,![]() ),试判断
),试判断![]() 是否为“1距”增函数,并说明理由;
是否为“1距”增函数,并说明理由;
(2)若![]() ,
,![]() R是“a距”增函数,求a的取值范围;
R是“a距”增函数,求a的取值范围;
(3)若![]() ,
,![]() (﹣1,
(﹣1,![]() ),其中k
),其中k![]() R,且为“2距”增函数,求
R,且为“2距”增函数,求![]() 的最小值.
的最小值.
【答案】(1)见解析; (2)![]() ; (3)
; (3)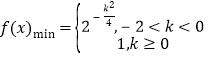 .
.
【解析】
(1)利用“1距”增函数的定义证明![]() 即可;(2)由“a距”增函数的定义得到
即可;(2)由“a距”增函数的定义得到![]() 在
在![]() 上恒成立,求出a的取值范围即可;(3)由
上恒成立,求出a的取值范围即可;(3)由![]() 为“2距”增函数可得到
为“2距”增函数可得到![]() 在
在![]() 恒成立,从而得到
恒成立,从而得到![]() 恒成立,分类讨论可得到
恒成立,分类讨论可得到![]() 的取值范围,再由
的取值范围,再由![]() ,可讨论出
,可讨论出![]() 的最小值。
的最小值。
(1)任意![]() ,
,![]() ,
,
因为![]() ,
,![]() , 所以
, 所以![]() ,所以
,所以![]() ,即
,即![]() 是“1距”增函数。
是“1距”增函数。
(2)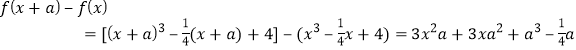 .
.
因为![]() 是“
是“![]() 距”增函数,所以
距”增函数,所以![]() 恒成立,
恒成立,
因为![]() ,所以
,所以![]() 在
在![]() 上恒成立,
上恒成立,
所以![]() ,解得
,解得![]() ,因为
,因为![]() ,所以
,所以![]() .
.
(3)因为![]() ,
,![]() ,且为“2距”增函数,
,且为“2距”增函数,
所以![]() 时,
时,![]() 恒成立,
恒成立,
即![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() 恒成立,
恒成立,
所以![]() , 得
, 得![]() ;
;
当![]() 时,
时,![]() ,
,
得![]() 恒成立,
恒成立,
所以![]() ,得
,得![]() ,
,
综上所述,得![]() .
.
又![]() ,
,
因为![]() ,所以
,所以![]() ,
,
当![]() 时,若
时,若![]() ,
,![]() 取最小值为
取最小值为![]() ;
;
当![]() 时,若
时,若![]() ,
,![]() 取最小值.
取最小值.
因为![]() 在R上是单调递增函数,
在R上是单调递增函数,
所以当![]() ,
,![]() 的最小值为
的最小值为![]() ;当
;当![]() 时
时![]() 的最小值为
的最小值为![]() ,
,
即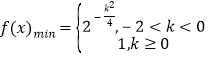 .
.


科目:高中数学 来源: 题型:
【题目】2017年春节期间,某服装超市举办了一次有奖促销活动,消费每超过600元(含600元),均可抽奖一次,抽奖方案有两种,顾客只能选择其中的一种.
方案一:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,一次性摸出3个球,其中奖规则为:若摸到3个红球,享受免单优惠;若摸出2个红球则打6折,若摸出1个红球,则打7折;若没摸出红球,则不打折.
方案二:从装有10个形状、大小完全相同的小球(其中红球3个,黑球7个)的抽奖盒中,有放回每次摸取1球,连摸3次,每摸到1次红球,立减200元.
(1)若两个顾客均分别消费了600元,且均选择抽奖方案一,试求两位顾客均享受免单优惠的概率;
(2)若某顾客消费恰好满1000元,试从概率的角度比较该顾客选择哪一种抽奖方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某射击运动员每次击中目标的概率都是0.8,现采用随机模拟的方法估计该运动员射击4次,至少击中3次的概率:先由计算器给出0到9之间取整数值的随机数,指定0,1表示没有击中目标,2,3,4,5,6,7,8,9表示击中目标,以4个随机数为一组,代表射击4次的结果,经随机模拟产生了20组随机数,根据以下数据估计该运动员射击4次,至少击中3次的概率为( )
7527 0293 7140 9857
0347 4373 8636 6947
1417 4698 0371 6233
2616 8045 6011 3661
9597 7424 7610 4281
A.0.852B.0.8192C.0.8D.0.75
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() 与点
与点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 过定点
过定点![]() ,且斜率为
,且斜率为![]() ,若椭圆
,若椭圆![]() 上存在
上存在![]() ,
,![]() 两点关于直线
两点关于直线![]() 对称,
对称,![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围及
的取值范围及![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数 ![]() 和
和![]() 的图象如图
的图象如图


给出下列四个命题:
①方程![]() 有且仅有
有且仅有![]() 个根;②方程
个根;②方程![]() 有且仅有
有且仅有![]() 个根;
个根;
③方程![]() 有且仅有
有且仅有![]() 个根;④方程
个根;④方程![]() 有且仅有
有且仅有![]() 个根;
个根;
其中正确命题的序号是( )
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某辆汽车以![]() 千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求
千米/小时的速度在高速公路上匀速行驶(考虑到高速公路行车安全要求![]() )时,每小时的油耗(所需要的汽油量)为
)时,每小时的油耗(所需要的汽油量)为![]() 升,其中
升,其中![]() 为常数,且
为常数,且![]() .
.
(1)若汽车以![]() 千米/小时的速度行驶时,每小时的油耗为
千米/小时的速度行驶时,每小时的油耗为![]() 升,欲使每小时的油耗不超过
升,欲使每小时的油耗不超过![]() 升,求
升,求![]() 的取值范围;
的取值范围;
(2)求该汽车行驶![]() 千米的油耗的最小值.
千米的油耗的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】扇形AOB中心角为![]() ,所在圆半径为
,所在圆半径为![]() ,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.
,它按如图(Ⅰ)(Ⅱ)两种方式有内接矩形CDEF.

(1)矩形CDEF的顶点C、D在扇形的半径OB上,顶点E在圆弧AB上,顶点F在半径OA上,设![]() ;
;
(2)点M是圆弧AB的中点,矩形CDEF的顶点D、E在圆弧AB上,且关于直线OM对称,顶点C、F分别在半径OB、OA上,设![]() ;
;
试研究(1)(2)两种方式下矩形面积的最大值,并说明两种方式下哪一种矩形面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)掷两枚质地均匀的骰子,计算点数和为7的概率;
(2)利用随机模拟的方法,试验120次,计算出现点数和为7的频率;
(3)所得频率与概率相差大吗?为什么会有这种差异?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com