
 如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形ABCD的面积为32$\sqrt{3}$.
如图,椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,直线x=±a和y=±b所围成的矩形ABCD的面积为32$\sqrt{3}$.分析 (1)根据条件可以得到关于a,b的方程组:$\left\{\begin{array}{l}{\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{4}}\\{4ab=32\sqrt{3}}\end{array}\right.$,这样可解出a,b,从而得出椭圆的方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)可设直线方程为y=k(x-1),联立椭圆的方程并消去y可得到(3+4k2)x2-8k2x+4k2-48=0,可设E(x1,y1),F(x2,y2),根据韦达定理便可得到${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{k}^{2}-48}{3+4{k}^{2}}$,这样便可求出$\overrightarrow{NE}•\overrightarrow{NF}=\frac{-45(1+{k}^{2})}{3+4{k}^{2}}$,从而可建立关于k的不等式,解不等式便可得出直线斜率的取值范围.
解答 解:(1)$e=\frac{c}{a}=\frac{1}{2}$;
∴$\frac{{a}^{2}-{b}^{2}}{{a}^{2}}=\frac{1}{4}$①;
矩形ABCD面积为$32\sqrt{3}$,即$2a•2b=32\sqrt{3}$②;
由①②解得:a2=16,b2=12;
∴椭圆M的标准方程是$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)设直线的方程为:y=k(x-1);
由$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}=48}\end{array}\right.$得,(3+4k2)x2-8k2x+4k2-48=0;
设E(x1,y1),F(x2,y2),则:
${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{3+4{k}^{2}},{x}_{1}{x}_{2}=\frac{4{k}^{2}-48}{3+4{k}^{2}}$;
又$\overrightarrow{NE}=({x}_{1}-1,{y}_{1}),\overrightarrow{NF}=({x}_{2}-1,{y}_{2})$;
∴$\overrightarrow{NE}•\overrightarrow{NF}=({x}_{1}-1)({x}_{2}-1)+{y}_{1}{y}_{2}$=(x1-1)(x2-1)+k(x1-1)•k(x2-1)
=(1+k2)(x1-1)(x2-1)
=(1+k2)[x1x2-(x1+x2)+1]
=$\frac{-45(1+{k}^{2})}{3+4{k}^{2}}$;
∴$-\frac{27}{2}≤\frac{-45(1+{k}^{2})}{3+4{k}^{2}}≤-12$;
解之得:$\frac{1}{2}≤{k}^{2}≤3$;
∴直线的斜率的取值范围为$[-\sqrt{3},-\frac{\sqrt{2}}{2}]∪[\frac{\sqrt{2}}{2},\sqrt{3}]$.
点评 考查椭圆的标准方程,椭圆的离心率,直线的点斜式方程,以及韦达定理,根据点的坐标求向量的坐标,数量积的坐标运算,一元二次不等式的解法.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
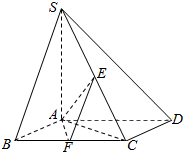 如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.
如图,已知四棱锥S-ABCD,底面ABCD为菱形,SA⊥平面ABCD,∠ADC=60°,E,F分别是SC,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{\sqrt{2}}{2}$ | B. | 1+$\frac{\sqrt{2}}{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x1+x2=2 | B. | 9<x3•x4<25 | C. | 0<(6-x3)•(6-x4)<1 | D. | 1<x1•x2<9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
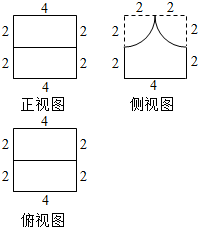 某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )
某几何体的三视图如图所示(其中侧视图为正方形上半部分在两个角上各截去四分之一圆),则该几何体的表面积为( )| A. | 48+4π | B. | 48+8π | C. | 64+4π | D. | 64+8π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com