
分析 (1)设选手甲任答一题正确的概率为p,根据答题连续两次答错的概率列出关于P的方程,得到甲答对题目的概率;
(2)选手甲能够进入决赛包括三种种情况,这三种情况是互斥的,由互斥事件的概率公式计算得到答案;
(3)由题意知X可取3,4,5,结合变量对应的事件和独立重复试验的概率公式写出变量的概率,写出分布列做出期望.
解答 解:(1)设甲答对一个问题的正确为P1,则(1-P1)2=$\frac{1}{9}$,解得P1=$\frac{2}{3}$.
(2)甲答完三题进入决赛的概率为${(\frac{2}{3})^3}=\frac{8}{27}$,
甲答完四题进入决赛的概率为$C_3^2{(\frac{2}{3})^2}•(\frac{1}{3})•(\frac{2}{3})=\frac{8}{27}$,
甲答完五题进入决赛的概率为$C_4^2{(\frac{2}{3})^2}•{(\frac{1}{3})^2}•(\frac{2}{3})=\frac{16}{81}$,
∴甲可以进入决定的概率为P=$\frac{8}{27}+\frac{8}{27}+\frac{16}{81}=\frac{64}{81}$.
(3)X的分布列为:
| X | 3 | 4 | 5 |
| P | $\frac{1}{3}$ | $\frac{10}{27}$ | $\frac{8}{27}$ |
点评 本题考查等可能事件的概率,考查离散型随机变量的分布列和期望,考查独立重复试验的概率公式,本题是一个综合题目,考查的知识点比较全面,在应用独立重复试验的概率公式时,注意数字运算不要出错.


科目:高中数学 来源: 题型:填空题
 一个大风车的半径为8米,按逆时针方向12分钟旋转一周,它的最低点离地面高2米,如图所示,设风车翼片的一个端点P离地面的距离为h(m),P的初始位置在最低点.风车转动的时间为t(min),当t=8(min)时,h=14(m); h与t的函数关系为$h(t)=-8cos\frac{π}{6}t+10$.
一个大风车的半径为8米,按逆时针方向12分钟旋转一周,它的最低点离地面高2米,如图所示,设风车翼片的一个端点P离地面的距离为h(m),P的初始位置在最低点.风车转动的时间为t(min),当t=8(min)时,h=14(m); h与t的函数关系为$h(t)=-8cos\frac{π}{6}t+10$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
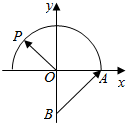 如图,已知点O(0,0),A(1,0),B(0,-1),P是曲线y=$\sqrt{1-{x}^{2}}$上一个动点,则$\overrightarrow{OP}$•$\overrightarrow{BA}$的取值范围是[-1,$\sqrt{2}$].
如图,已知点O(0,0),A(1,0),B(0,-1),P是曲线y=$\sqrt{1-{x}^{2}}$上一个动点,则$\overrightarrow{OP}$•$\overrightarrow{BA}$的取值范围是[-1,$\sqrt{2}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条直线 | B. | 两条直线 | C. | 一条射线 | D. | 一条线段 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com