
(本小题15分)已知函数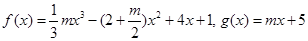 .
.
(1)当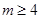 时,求
时,求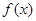 的单调递增区间;
的单调递增区间;
(2)是否存在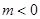 ,使得对任意的
,使得对任意的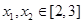 ,都有
,都有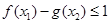 恒成立.若存在,求出
恒成立.若存在,求出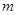 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
(1) 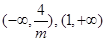 。(2)存在,
。(2)存在,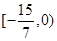
解析试题分析:(1)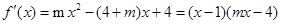
当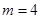 时,
时,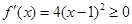 , ∴
, ∴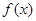 在
在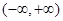 上单增, …………………2分
上单增, …………………2分
当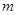 >4时,
>4时,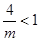 , ∴
, ∴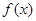 的递增区间为
的递增区间为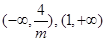 …….6.分
…….6.分
(2)假设存在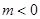 ,使得命题成立,此时
,使得命题成立,此时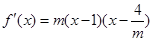 .
.
∵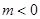 , ∴
, ∴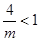 .
.
则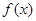 在
在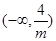 和
和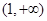 递减,在
递减,在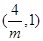 递增.
递增.
∴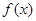 在[2,3]上单减,又
在[2,3]上单减,又 在[2,3]单减.
在[2,3]单减.
∴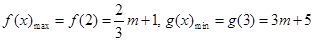 . …………………10分
. …………………10分
因此,对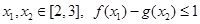 恒成立.
恒成立.
即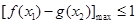 , 亦即
, 亦即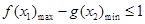 恒成立.
恒成立.
∴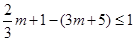 ∴
∴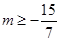 . 又
. 又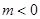 故
故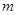 的范围为
的范围为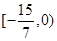 ...15分
...15分
考点:本题考查利用导数求函数的单调区间、导数在最大值、最小值问题中的应用及恒成立的问题。
点评:利用导数研究含参函数的单调区间,关键是解不等式,因此要研究含参不等式的解法,应注意对参数的讨论;研究是否存在问题,通常先假设存在,转化为封闭性问题,对于恒成立问题,一般应利用到函数的最值,而最值的确定又通常利用导数的方法解决.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知方程
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某炮兵阵地位于地面A处,两观察所分别位于地面点C和D处, 已知CD=6000m,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.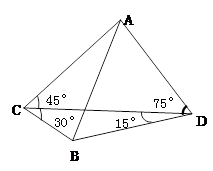
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(16分)已知函数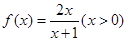
(1)求证:函数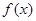 在
在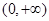 上为单调增函数;
上为单调增函数;
(2)设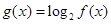 ,求
,求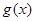 的值域;
的值域;
(3)对于(2)中函数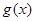 ,若关于
,若关于 的方程
的方程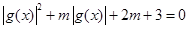 有三个不同的实数解,求
有三个不同的实数解,求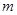 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com