
(12分)已知函数 ,
, 是
是 的一个极值点.
的一个极值点.
(1)求 的单调递增区间;
的单调递增区间;
(2)若当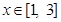 时,
时,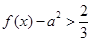 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)函数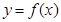 的单调递增区间为
的单调递增区间为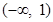 ,
,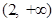 . (Ⅱ)
. (Ⅱ)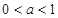 .
.
解析试题分析:(I)先求导函数,然后根据x=2是f(x)的一个极值点建立等式关系,求出b,然后解不等式f′(x)>0即可求出函数的单调增区间;
(II)先利用导数求出函数f(x)在区间[1,3]上的最小值,若当x∈[1,3]时,要使f(x)-a2> 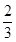
恒成立,只需f(x) min>a2+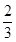 ,即可求出a的范围.
,即可求出a的范围.
解:(Ⅰ)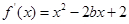 . ∵
. ∵ 是
是 的一个极值点,
的一个极值点,
∴ 是方程
是方程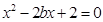 的一个根,解得
的一个根,解得 .
.
令 ,则
,则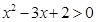 ,解得
,解得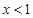 或
或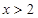 .
.
∴函数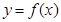 的单调递增区间为
的单调递增区间为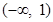 ,
,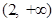 .
.
(Ⅱ)∵当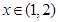 时
时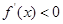 ,
,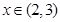 时
时 ,
,
∴ 在(1,2)上单调递减,
在(1,2)上单调递减, 在(2,3)上单调递增.
在(2,3)上单调递增.
∴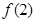 是
是 在区间[1,3]上的最小值,且
在区间[1,3]上的最小值,且 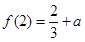 .
.
若当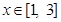 时,要使
时,要使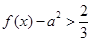 恒成立,只需
恒成立,只需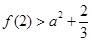 ,
,
即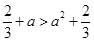 ,解得
,解得 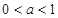 .
.
考点:本题主要考查了函数的极值,单调性和在闭区间上的最值,同时考查了恒成立问题,属于中档题
点评:解决该试题的关键是利用极值点处导数为零,那么得到参数b的值,然后求解二次不等式同时能将不等式的恒成立问题,转换为求解函数的最小值大于参数问题。即f(x) min>a2+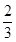 体现了转换与化归思想的和运用。
体现了转换与化归思想的和运用。


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知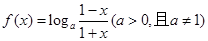
(1)求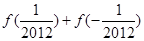 的值;
的值;
(2)当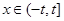 (其中
(其中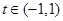 ,且
,且 为常数)时,
为常数)时,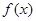 是否存在最小值,如果存在求出最小值;如
是否存在最小值,如果存在求出最小值;如
果不存在,请说明理由;
(3)当 时,求满足不等式
时,求满足不等式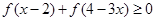 的
的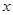 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题15分)已知函数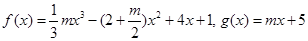 .
.
(1)当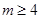 时,求
时,求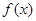 的单调递增区间;
的单调递增区间;
(2)是否存在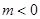 ,使得对任意的
,使得对任意的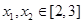 ,都有
,都有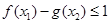 恒成立.若存在,求出
恒成立.若存在,求出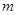 的取值范围; 若不存在,请说明理由.
的取值范围; 若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)星期天,刘先生到电信局打算上网开户,经询问,记录了可能需要的三种方式所花费的费用资料,现将资料整理如下:
1163普通:上网资费2元/小时;
2163A:每月50元(可上网50小时),超过50小时的部分资费2元/小时;
3ADSLD:每月70元,时长不限(其他因素忽略不计).
请你用所学的函数知识对上网方式与费用问题作出研究:
(1)分别写出三种上网方式中所用资费与时间的函数解析式;
(2)在同一坐标系内分别画出三种方式所需资费与时间的函数图象;
(3)根据你的研究,请给刘先生一个合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com