
(本题满分12分)
已知函数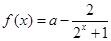 (其中常数
(其中常数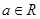 )
)
(1)判断函数 的单调性,并加以证明;
的单调性,并加以证明;
(2)如果 是奇函数,求实数
是奇函数,求实数 的值。
的值。
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(本小题满分15分)已知函数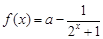 ,
,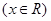 .
.
(1)用定义证明:不论 为何实数
为何实数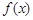 在
在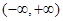 上为增函数;
上为增函数;
(2)若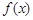 为奇函数,求
为奇函数,求 的值;
的值;
(3)在(2)的条件下,求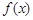 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知f (x)=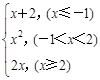 .
.
(1)求函数f (x)的值域.
(2)若f (t)=3,求t的值.
(3)用单调性定义证明在[2,+∞)上单调递增.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知方程
 (
( 为实数)有两个不相等的实数根,分别求:
为实数)有两个不相等的实数根,分别求:
(Ⅰ)若方程 的根为一正一负,则求实数
的根为一正一负,则求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 的两根都在
的两根都在 内,则求实数
内,则求实数 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某炮兵阵地位于地面A处,两观察所分别位于地面点C和D处, 已知CD=6000m,∠ACD=45°,∠ADC=75°, 目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图),求炮兵阵地到目标的距离.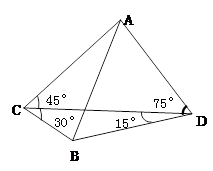
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com