
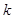 和
和 ,使得函数
,使得函数 和
和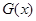 对其公共定义域上的任意实数
对其公共定义域上的任意实数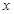 都满足:
都满足: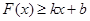 和
和 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和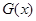 的“隔离直线”.已知函数
的“隔离直线”.已知函数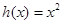 ,
, 为自然对数的底数),
为自然对数的底数), ,
,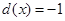 .有下列命题:①
.有下列命题:① 在
在 递减;②
递减;②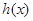 和
和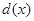 存在唯一的“隔离直线”;③
存在唯一的“隔离直线”;③ 和
和 存在“隔离直线”
存在“隔离直线” ,且
,且 的最大值为
的最大值为 ;④函数
;④函数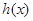 和
和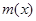 存在唯一的隔离直线
存在唯一的隔离直线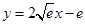 .其中真命题的个数
.其中真命题的个数 A.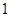 个 个 | B. 个 个 | C. 个 个 | D.个 |
科目:高中数学 来源:不详 题型:单选题
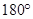 ,归纳出所有三角形的内角和都是
,归纳出所有三角形的内角和都是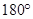 ;
;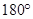 ,四边形内角和是
,四边形内角和是 ,五边形内角和是
,五边形内角和是 ,由此得凸多边形内角和是
,由此得凸多边形内角和是
| A.(1)(2) | B.(1)(3) | C.(1)(2)(4) | D.(2)(4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
 ,若
,若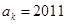 ,则
,则 .
. | |
| 图-1 | 图-2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
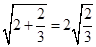 ,
,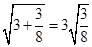 ,
,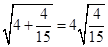 ,。。。,若
,。。。,若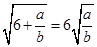 (a , b
(a , b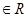 ) , 则( )
) , 则( )| A.a=5, b=24 | B.a=6, b=24 |
| C.a=6, b=35 | D.a=5, b=35 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.① | B.② | C.①② | D.③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com