
【题目】高铁、移动支付、网购与共享单车被称为中国的新四大发明,为了解永安共享单车在淮南市的使用情况,永安公司调查了100辆共享单车每天使用时间的情况,得到了如图所示的频率分布直方图.
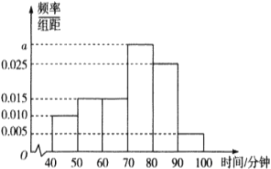
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现在用分层抽样的方法从前3组中随机抽取8辆永安共享单车,将该样本看成一个总体,从中随机抽取2辆,求其中恰有1辆的使用时间不低于50分钟的概率;
(Ⅲ)为进一步了解淮南市对永安共享单车的使用情况,永安公司随机抽取了200人进行调查问卷分析,得到如下2×2列联表:
经常使用 | 偶尔使用或不用 | 合计 | |
男性 | 50 | 100 | |
女性 | 40 | ||
合计 | 200 |
完成上述2×2列联表,并根据表中的数据判断是否有85%的把握认为淮南市使用永安共享单车的情况与性别有关?
附: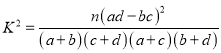
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)表见解析,没有85%的把握认为淮南市使用永安共享单车的情况与性别有关.
;(Ⅲ)表见解析,没有85%的把握认为淮南市使用永安共享单车的情况与性别有关.
【解析】
(Ⅰ)根据频率分布直方图中的面积之和为1,求参数![]() .
.
(Ⅱ)由题意前三组的频率比为2:3:3,所以由分层抽样可知前三组抽取的单车辆数分别为2,3,3,利用列举的方法可求得概率.
(Ⅲ)先计算填好2×2列联表,然后代入公式计算![]() ,与给出的表格比较得出答案.
,与给出的表格比较得出答案.
(Ⅰ)由题意![]() 解得
解得![]() .
.
(Ⅱ)由频率分布直方图可知,前三组的频率比为2:3:3,所以由分层抽样可知前三组抽取的单车辆数分别为2,3,3,分别记为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,从中抽取2辆的结果有:
,从中抽取2辆的结果有:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ;
;
共28个,恰有1辆的使用时间不低于50分钟的结果有12个,
∴所求的概率为![]() .
.
(Ⅲ)2×2列联表如下:
经常使用 | 偶尔使用或不用 | 合计 | |
男性 | 50 | 50 | 100 |
女性 | 60 | 40 | 100 |
合计 | 110 | 90 | 200 |
由上表及公式可知![]() ,因为2.02<2.072
,因为2.02<2.072
所以没有85%的把握认为淮南市使用永安共享单车的情况与性别有关.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,…,
,…,![]() 是由
是由![]() (
(![]() )个整数
)个整数![]() ,
,![]() ,…,
,…,![]() 按任意次序排列而成的数列,数列
按任意次序排列而成的数列,数列![]() 满足
满足![]() (
(![]() ).
).
(1)当![]() 时,写出数列
时,写出数列![]() 和
和![]() ,使得
,使得![]() .
.
(2)证明:当![]() 为正偶数时,不存在满足
为正偶数时,不存在满足![]() (
(![]() )的数列
)的数列![]() .
.
(3)若![]() ,
,![]() ,…,
,…,![]() 是
是![]() ,
,![]() ,…,
,…,![]() 按从大到小的顺序排列而成的数列,写出
按从大到小的顺序排列而成的数列,写出![]() (
(![]() ),并用含
),并用含![]() 的式子表示
的式子表示![]() .
.
(参考:![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程
的参数方程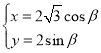 (
(![]() 为参数).直线
为参数).直线![]() 的参数方程
的参数方程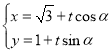 (
(![]() 为参数).
为参数).
(Ⅰ)求曲线![]() 在直角坐标系中的普通方程;
在直角坐标系中的普通方程;
(Ⅱ)以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,当曲线
轴的正半轴为极轴建立极坐标系,当曲线![]() 截直线
截直线![]() 所得线段的中点极坐标为
所得线段的中点极坐标为![]() 时,求直线
时,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两动圆![]() 和
和![]() (
(![]() ),把它们的公共点的轨迹记为曲线
),把它们的公共点的轨迹记为曲线![]() ,若曲线
,若曲线![]() 与
与![]() 轴的正半轴的交点为
轴的正半轴的交点为![]() ,且曲线
,且曲线![]() 上的相异两点
上的相异两点![]() 满足:
满足:![]() .
.
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)证明直线![]() 恒经过一定点,并求此定点的坐标;
恒经过一定点,并求此定点的坐标;
(3)求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com