
(本小题满分12分)如图,已知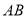 是圆
是圆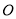 的直径,
的直径, ,
,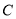 是⊙
是⊙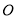 上一点,且
上一点,且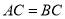 ,
,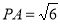 ,
,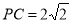 ,
,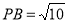
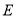 是
是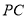 的中点,
的中点,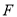 是
是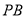 的中点
的中点
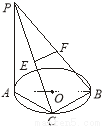
(1)求证: 平面
平面 ;
;
(2)求证: 平面
平面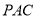 ;
;
(3)求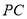 与平面
与平面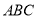 所成角的大小
所成角的大小
(1)证明见解析;(2)证明见解析;(3)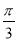
【解析】
试题分析:(1)证明线面平行常用方法:一是利用线面平行的判定定理,二是利用面面平行的性质定理,三是利用面面平行的性质;(2)证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高,中线和顶角的角平分线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形等等;(3)证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中的一条垂直于这个平面,则另一条也垂直于这个平面.解题时,注意线线、线面与面面关系的相互转化;(4)证明两个平面垂直,首先考虑直线与平面垂直,也可以简单记为“证面面垂直,找线面垂直”,是化归思想的体现,这种思想方法与空间中的平行关系的证明类似,掌握化归与转化思想方法是解决这类题的关键.
试题解析:证明:(1)在?PBC中,E是PC的中点,F是PB的中点,所以EF//BC. (1分)
又BC?平面ABC,EF?平面ABC,所以EF//平面ABC. (3分)
(2)因为AB是⊙O的直径,所以BC?AC. (4分)
在Rt?ABC中,AB=2,AC=BC,所以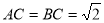 . (5分)
. (5分)
因为在?PCB中, ,
, ,
, ,
,
所以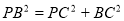 ,所以BC?PC. (6分)
,所以BC?PC. (6分)
又PC∩AC=C,所以BC?平面PAC. (7分)
由(1)知EF//BC,所以EF?平面PAC. (8分)
(3)【解析】
由(2)知BC?平面PAC,PA?平面PAC,所以PA?BC. (9分)
因为在?PAC中, ,
,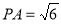 ,
,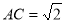 ,
,
所以 ,所以PA?AC. (10分)
,所以PA?AC. (10分)
又AC∩BC=C,所以PA?平面ABC.
所以?PCA为PC与平面ABC所成角. (11分)
在Rt PAC中,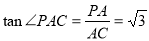 ,所以?PCA=
,所以?PCA= ,
,
即PC与平面ABC所成角的大小为 . (12分)
. (12分)
考点:1、直线与平面平行的判定;2、直线与平面垂直的判定;3、直线与平面所成的角.


科目:高中数学 来源:2014-2015学年河北邢台一中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知 是抛物线
是抛物线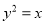 的焦点,
的焦点, 是该抛物线上的两点,
是该抛物线上的两点,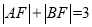 ,则线段
,则线段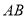 的中点到
的中点到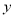 轴的距离为 ( )
轴的距离为 ( )
A.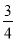 B.1 C.
B.1 C.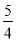 D.
D.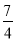
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:选择题
已知三个正态分布密度函数 (
(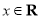 ,
,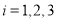 )的图象如图
)的图象如图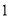 所示,则( )
所示,则( )

A. ,
,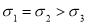
B.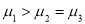 ,
,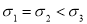
C. ,
,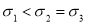
D.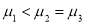 ,
,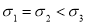
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图输出的结果是
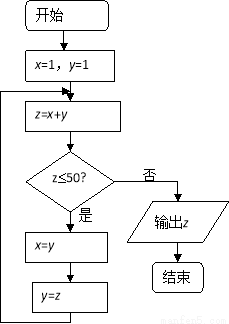
A.55 B.65
C.78 D.89
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:选择题
已知全集U={1,2,3,4,5,6},集合M={1,3,5},则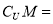
A.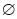 B.{1,3,5} C.{2,4,6} D.{1,2,3,4,5,6}
B.{1,3,5} C.{2,4,6} D.{1,2,3,4,5,6}
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:选择题
设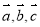 是非零向量,已知命题p:若
是非零向量,已知命题p:若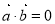 ,
,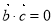 ,则
,则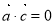 ;命题q:若
;命题q:若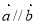 ,
,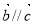 ,则
,则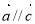 . 则下列命题中真命题是
. 则下列命题中真命题是
A. B.
B.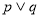 C.
C.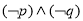 D.
D.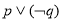
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考文科数学试卷(解析版) 题型:选择题
程序框图如下图所示,则输出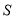 的值为( )
的值为( )
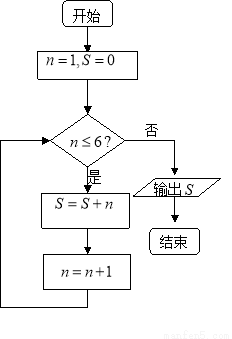
A.15 B.21 C.22 D.28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com