练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价，又不高于800元/件，经试销调查，发现销售量y（件）与销售单价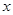（元/件），可近似看做一次函数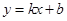的关系（如下图所示）.

    （1）根据图象，求一次函数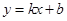的表达式；

    （2）设公司获得的毛利润（毛利润＝销售总价－成本总价）为S元,

    ①求S关于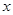的函数表达式；

    ②求该公司可获得的最大毛利润，并求出相应的销售单价.

     

     

     

    【答案】

    （1）由图象知，当x=600时，y=400，当x=700时，y=300，代入中，得，解得.

    ∴      ------------4分

    (2)依题意得，

    .------------10分

    ∴当时，       ------------12分

    答：该公司可获得的最大毛利润是62500元，相应的销售单价为750元

    【解析】略

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y（件）与销售单价x（元）之间的关系可近似看作一次函数y=kx+b（k≠0），函数图象如图所示．
    （1）根据图象，求一次函数y=kx+b（k≠0）的表达式；
    （2）设公司获得的毛利润（毛利润=销售总价-成本总价）为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    某公司试销一种成本单价为500元/件的新产品，规定试销时销售单价不低于成本单价又不高于800元/件，经试销调查，发现销售量y（件）与销售单价x（元/件），可近似看做一次函数y=kx+b的关系（如图所示）．
    （Ⅰ）根据图象，求一次函数y=kx+b的表达式；
    （Ⅱ）设公司获得的利润（利润=销售总价-成本总价）为S元，写出S关于x的函数表达式，并求该公司可获得的最大利润．

    查看答案和解析>>

    科目：高中数学 来源：2012年人教A版高中数学必修一3.2函数模型及其应用练习卷（二）（解析版） 题型：解答题

    某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y＝kx＋b(k≠0)，函数图象如图所示．

    (1)根据图象，求一次函数y＝kx＋b(k≠0)的表达式；

    (2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

     

    查看答案和解析>>

    科目：高中数学 来源：2014届北京市高一上学期期中考试数学 题型：解答题

    （本小题满分14分）某公司试销一种成本单价为500元的新产品，规定试销时销售单价不低于成本单价，又不高于800元．经试销调查，发现销售量y(件)与销售单价x(元)之间的关系可近似看作一次函数y＝kx＋b(k≠0)，函数图象如图所示．

    (1)根据图象，求一次函数y＝kx＋b(k≠0)的表达式；

    (2)设公司获得的毛利润(毛利润＝销售总价－成本总价)为S元．试问销售单价定为多少时，该公司可获得最大毛利润？最大毛利润是多少？此时的销售量是多少？

     

     

    查看答案和解析>>

    同步练习册答案