
分析 令g(x)=f(x)-$\frac{1}{4}$x2,求出函数的奇偶性和单调性,问题转化为g(4-m)≥g(m),根据函数的单调性求出m的范围即可.
解答 解:令g(x)=f(x)-$\frac{1}{4}$x2,
g′(x)=f′(x)-$\frac{x}{2}$,
当x∈(0,+∞)时,f′(x)<$\frac{x}{2}$,
∴g(x)在(0,+∞)递减,
而g(-x)=f(-x)-$\frac{1}{4}$x2,
∴f(-x)+f(x)=g(-x)+$\frac{1}{4}$x2+g(x)+$\frac{1}{4}$x2=$\frac{{x}^{2}}{2}$,
∴g(-x)+g(x)=0,
∴g(x)是奇函数,g(x)在R递减,
若f(4-m)-f(m)≥4-2m,
则f(4-m)-$\frac{1}{4}$(4-m)2≥f(m)-$\frac{1}{4}$m2,
∴g(4-m)≥g(m),
∴4-m≤m,解得:m≥2,
故答案为:[2,+∞).
点评 本题考查了函数的单调性、奇偶性问题,考查导数的应用,是一道中档题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:填空题
已知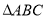 为等腰直角三角形,斜边
为等腰直角三角形,斜边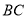 上的中线
上的中线 ,将
,将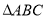 沿
沿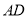 折成
折成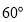 的二面角,连结
的二面角,连结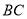 ,则三棱锥
,则三棱锥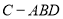 的体积为__________.
的体积为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
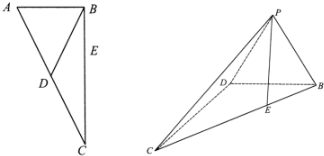 如图,直角三角形ABC中,∠A=60°,∠ABC=90°,AB=2,E为线段BC上一点,且BE=$\frac{1}{3}$BC,沿AC边上的中线BD将△ABD折起到△PBD的位置.
如图,直角三角形ABC中,∠A=60°,∠ABC=90°,AB=2,E为线段BC上一点,且BE=$\frac{1}{3}$BC,沿AC边上的中线BD将△ABD折起到△PBD的位置.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com