
已知函数![]() .
.
(1)如果a>0,函数在区间![]() 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;
(2)当x≥1时,不等式![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
考点:
实际问题中导数的意义;函数在某点取得极值的条件.
专题:
压轴题;导数的综合应用.
分析:
(1)因为![]() ,x>0,x>0,则
,x>0,x>0,则![]() ,利用函数的单调性和函数f(x)在区间(a,a+
,利用函数的单调性和函数f(x)在区间(a,a+![]() )(其中a>0)上存在极值,能求出实数a的取值范围.
)(其中a>0)上存在极值,能求出实数a的取值范围.
(2)不等式![]() ,即为
,即为![]() ,构造函数
,构造函数![]() ,利用导数知识能求出实数k的取值范围.
,利用导数知识能求出实数k的取值范围.
解答:
解:(1)因为![]() ,x>0,则
,x>0,则![]() ,(1分)
,(1分)
当0<x<1时,f'(x)>0;
当x>1时,f'(x)<0.
所以f(x)在(0,1)上单调递增;在(1,+∞)上单调递减,所以函数f(x)在x=1处取得极大值.
因为函数f(x)在区间(a,a+![]() )(其中a>0)上存在极值,
)(其中a>0)上存在极值,
所以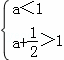 解得
解得![]() .
.
(2)不等式![]() ,即为
,即为![]() ,记
,记![]() ,
,
所以![]() =
=![]()
令h(x)=x﹣lnx,
则![]() ,∵x≥1,∴h'(x)≥0,∴h(x)在[1,+∞)上单调递增,∴[h(x)]min=h(1)=1>0,
,∵x≥1,∴h'(x)≥0,∴h(x)在[1,+∞)上单调递增,∴[h(x)]min=h(1)=1>0,
从而g'(x)>0,
故g(x)在[1,+∞)上也单调递增,所以[g(x)]min=g(1)=2,
所以k≤2.
点评:
本题考查极值的应用,应用满足条件的实数的取值范围的求法.解题时要认真审题,仔细解答,注意构造法和分类讨论法的合理运用.


科目:高中数学 来源: 题型:
| 2 |
| x |
| 5 |
| 3 |
| 11 |
| 5 |
| 5 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2006-2007学年浙江省宁波市鄞州高级中学高三(下)第一次月考数学试卷(解析版) 题型:解答题
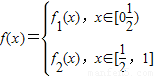 其中
其中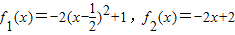
 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,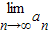 ;
;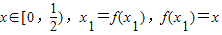 ,求x
,求x
查看答案和解析>>
科目:高中数学 来源:2000年北京市高考数学试卷(理)(解析版) 题型:解答题
 其中
其中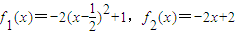
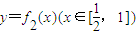 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,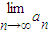 ;
; ,求x
,求x
查看答案和解析>>
科目:高中数学 来源:2000年安徽省高考数学试卷(理)(解析版) 题型:解答题
 其中
其中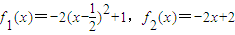
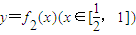 的反函数为y=g(x),a1=1,a2=g(a1),…,
的反函数为y=g(x),a1=1,a2=g(a1),…,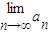 ;
;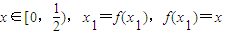 ,求x
,求x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com