练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    Rt△ABC中，斜边BC为m，以BC的中点O为圆心作直径为n （n＜数学公式）的圆，分别交BC于P，Q两点，求|AP|2+|AQ|2+|PQ|2的值．

    解：由题意，OA=OB=，OP=OQ=n
    △AOP中，根据余弦定理AP2=OA2+OP2-2OA•OPcos∠AOP
    同理△AOQ中，AQ2=OA2+OQ2-2OA•OQcos∠AOQ
    因为∠AOP+∠AOQ=180°，
    所以|AP|2+|AQ|2+|PQ|2=2OA2+2OP2+PQ2=2（）2+2n2+（2n）2=+6n2．
    分析：利用余弦定理，求出|AP|2、|AQ|2，结合∠AOP+∠AOQ=180°，即可求|AP|2+|AQ|2+|PQ|2的值．
    点评：本题考查直线与圆的位置关系，考查余弦定理的运用，考查学生的计算能力，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    等腰Rt△ABC中，斜边BC=4
    		2
    ，一个椭圆以C为其中一个焦点，另一焦点在线段AB上，且椭圆经过A，B两点，则该椭圆的离心率是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在Rt△ABC中，斜边AB的长为2，则△ABC的面积的最大值为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    Rt△ABC中，斜边BC为m，以BC的中点O为圆心作直径为n （n＜
    m2
    ）的圆，分别交BC于P，Q两点，求|AP|2+|AQ|2+|PQ|2的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

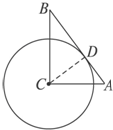    （2013•肇庆二模）（几何证明选讲选做题）
    如图，在Rt△ABC中，斜边AB=12，直角边AC=6，如果以C为圆心的圆与AB相切于D，则⊙C的半径长为
    3
    		3
    3
    		3
    ．

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年安徽省蚌埠四校联盟高一自主招生考试数学试卷（解析版） 题型：填空题

    已知：如图，在Rt△ABC中，斜边AB＝5厘米，BC＝a厘米，AC＝b厘米，a＞b，且a、b是方程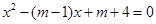的两根，

    ⑴求a和b的值；

    ⑵△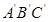与△ABC开始时完全重合，然后让△ABC固定不动，将

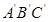    △以1厘米/秒的速度沿BC所在的直线向左移动.

    ⅰ)设x秒后△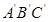与△ABC 的重叠部分的面积为y平方厘米，求y与x之间的函数关系式,并写出x的取值范围；

     ⅱ)几秒后重叠部分的面积等于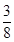平方厘米？

     

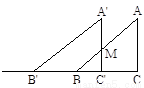
    查看答案和解析>>

    同步练习册答案