
分析 (1)利用导数求出单调性,即可求最值;(2)把交点代入,求出m的关系;求h′(αx1+βx2),利用构造函数的方法,证明问题.
解答 解:(1)当m=0时,f(x)=2lnx-x2,求导得${f^'}(x)=\frac{2(1+x)(1-x)}{x}$,很据定义域,容易得到在x=1处取得最大值,得到函数的最大值为-1.
(2)根据条件得到$2ln{x_1}-x_1^2-m{x_1}=0$,$2ln{x_2}-x_2^2-m{x_2}=0$,两式相减得$2(ln{x_1}-ln{x_2})-(x_1^2-x_2^2)=m({x_1}-{x_2})$,
得$m=\frac{{2(ln{x_1}-ln{x_2})-(x_1^2-x_2^2)}}{{{x_1}-{x_2}}}=\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}-({x_1}+{x_2})$,
因为${f^'}(x)=\frac{2}{x}-2x-m$,
得${f^'}(\frac{1}{3}{x_1}+\frac{2}{3}{x_2})=\frac{2}{{\frac{1}{3}{x_1}+\frac{2}{3}{x_2}}}-2(\frac{1}{3}{x_1}+\frac{2}{3}{x_2})-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}+({x_1}+{x_2})$=$\frac{2}{{\frac{1}{3}{x_1}+\frac{2}{3}{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}+\frac{1}{3}({x_1}-{x_2})$,
因为0<x1<x2,所以$\frac{1}{3}({x_1}-{x_2})<0$,要证${f^'}(\frac{1}{3}{x_1}+\frac{2}{3}{x_2})<0$,
即证$\frac{2}{{\frac{1}{3}{x_1}+\frac{2}{3}{x_2}}}-\frac{{2(ln{x_1}-ln{x_2})}}{{{x_1}-{x_2}}}<0$,
即证$\frac{{2({x_1}-{x_2})}}{{\frac{1}{3}{x_1}+\frac{2}{3}{x_2}}}-2(ln{x_1}-ln{x_2})>0$,即证$\frac{{2(1-\frac{x_2}{x_1})}}{{\frac{1}{3}+\frac{2}{3}\frac{x_2}{x_1}}}-2ln\frac{x_1}{x_2}>0$,
设$\frac{x_1}{x_2}=t$(0<t<1),原式即证$\frac{2(1-t)}{{\frac{1}{3}+\frac{2}{3}t}}-2lnt>0$,即证$\frac{6(1-t)}{1+2t}-2lnt>0$,
构造$g(t)=-3+\frac{9}{1+2t}-2lnt$求导很容易发现为负,g(t)单调减,所以g(t)>g(1)=0得证
点评 考察了导函数的应用和利用构造函数的方法,结合导数求不等式.难度较大,属于压轴题.


科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
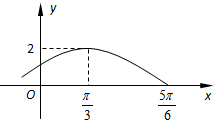 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则函数y=f(x)的解析式为$f(x)=2sin(x+\frac{π}{6})$.
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$,x∈R)的部分图象如图所示.则函数y=f(x)的解析式为$f(x)=2sin(x+\frac{π}{6})$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{10}{11}$ | C. | $\frac{11}{12}$ | D. | $\frac{32}{33}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1-e | B. | e-1 | C. | -1-e | D. | e+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com