
科目:高中数学 来源:2014-2015年河北保定一中高二下第一次段考理数学试卷(解析版) 题型:填空题
下面是关于复数z= 的四个命题:p1:|z|=2, p2:z2=2i, p3:z的共轭复数为1+i, p4:z的虚部为-1,其中真命题的个数为 .
的四个命题:p1:|z|=2, p2:z2=2i, p3:z的共轭复数为1+i, p4:z的虚部为-1,其中真命题的个数为 .
查看答案和解析>>
科目:高中数学 来源:2016届浙江省高三期中文科数学试卷(解析版) 题型:选择题
为了得到函数 的图象,只需把函数
的图象,只需把函数 的图象( )
的图象( )
A.向左平移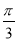 个单位长度
个单位长度
B.向右平移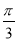 个单位长度
个单位长度
C.向左平移 个单位长度
个单位长度
D.向右平移 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在四棱柱 中,
中, ,底面
,底面 为菱形,
为菱形,
 ,已知
,已知 .
.

(1)求证:平面 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
【答案】(1)见解析;(2) .
.
【解析】
试题分析:(1)要证平面 平面
平面 ,即证
,即证 平面
平面 ,而
,而 可由菱形的性质得到,又由
可由菱形的性质得到,又由 底面
底面 ,得到
,得到 底面
底面 ,进而得到
,进而得到 ,从而使问题得证;(2)取
,从而使问题得证;(2)取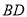 的中点
的中点 ,连接
,连接 ,
,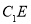 ,过
,过 作
作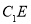 的垂线
的垂线 ,可知
,可知 为点
为点 到平面
到平面 的距离,从而通过解直角三角形求得
的距离,从而通过解直角三角形求得 的长.
的长.
试题解析:(1)依题意, 因为四棱柱 中,
中, 底面
底面 ,
,
所以 底面
底面 .
.
又 底面
底面 ,所以
,所以 .
.
因为 为菱形,所以
为菱形,所以 ,而
,而 ,所以
,所以 平面
平面 .
.
又 底面
底面 ,所以平面
,所以平面 平面
平面 .
.
(2)取 的中点
的中点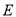 ,连接
,连接 ,
,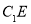 ,则
,则 ,
,

 ,故
,故
 ,
,
过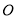 作
作 的垂线
的垂线 ,易证
,易证 ,即
,即 为点
为点 到平面
到平面 的距离.
的距离.
在直角三角形 中,
中, ,
, ,
, ,
,
所以 ,即点
,即点 到平面
到平面 的距离为
的距离为 .
.
考点:1、空间直线与平面的垂直的判定与性质;2、空间平面与平面垂直的判定;3、点到平面的距离.
【题型】解答题
【适用】一般
【标题】【百强校】2016届江西省临川一中高三上学期期中文科数学试卷(带解析)
【关键字标签】
【结束】
(本小题满分12分)已知函数 .
.
(1)当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)设函数 ,求函数
,求函数 的单调区间.
的单调区间.
查看答案和解析>>
科目:高中数学 来源:2016届江苏省高三周练数学试卷(解析版) 题型:解答题
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,椭圆上的点到焦点的距离的最小值为
轴上,椭圆上的点到焦点的距离的最小值为 ,离心率为
,离心率为 .
.

(1)求椭圆 的标准方程;
的标准方程;
(2)过点 作斜率为
作斜率为 的直线
的直线 交
交 于
于 、
、 两点,点
两点,点 是点
是点 关于
关于 轴的对称点,求证直线
轴的对称点,求证直线 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源:2016届吉林省高三上学期二模文科数学试卷(解析版) 题型:填空题
函数f(x)=ax3+bx2+cx+d的部分数值如下表:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
f(x) | -80 | -24 | 0 | 4 | 0 | 0 | 16 | 60 | 144 |
则函数y=lgf(x)的定义域为__________.
查看答案和解析>>
科目:高中数学 来源:2016届甘肃省高三上学期期中文科数学试卷(解析版) 题型:解答题
(本小题12分)根据国家环保部新修订的《环境空气质量标准》规定:居民区PM2.5的年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米.某城市环保部门随机抽取了一居民区去年20天PM2.5的24小时平均浓度的监测数据,数据统计如下:
]
组别 | PM2.5浓度(微克/立方米) | 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
(Ⅰ)从样本中PM2.5的24小时平均浓度超过50微克/立方米的5天中,随机抽取2天,求恰好有一天PM2.5的24小时平均浓度超过75微克/立方米的概率;
(Ⅱ)求样本平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年广东省深圳市高一上学期期中数学试卷(解析版) 题型:选择题
设函数 ,
, 的定义域都为R,且
的定义域都为R,且 是奇函数,
是奇函数, 是偶函数,则下列结论正确的是( ).
是偶函数,则下列结论正确的是( ).
A.
 是偶函数 B.|
是偶函数 B.| |
| 是奇函数
是奇函数
C. |
| |是奇函数 D.|
|是奇函数 D.|
 |是奇函数
|是奇函数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com