
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
分析 已知等式左边利用二倍角的余弦函数公式化简,右边整理后,得出cosB=$\frac{a}{2c}$①,利用余弦定理表示出cosB,代入等式化简得到b=c,即可判断三角形ABC形状.
解答 解:已知等式变形得:cosB+1=$\frac{a}{2c}$+1,
即cosB=$\frac{a}{2c}$①,
由余弦定理得:cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$,
代入①得:$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{a}{2c}$,
整理得:b2=c2,
即有b=c.
则△ABC为等腰三角形.
故选:C.
点评 此题考查了余弦定理,二倍角的余弦函数公式,熟练掌握余弦定理是解本题的关键,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 越接近于圆 | B. | 越扁 | ||
| C. | 先接近于圆后越扁 | D. | 先越扁后接近于圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 共线向量的方向相同 | B. | 零向量是$\overrightarrow{0}$ | ||
| C. | 长度相等的向量叫做相等向量 | D. | 共线向量是在一条直线上的向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | π | C. | $\frac{2π}{3}-\frac{{\sqrt{3}}}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,$\frac{π}{4}$) | B. | (2,$\frac{3π}{4}$) | C. | (2,-$\frac{π}{4}$) | D. | (2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
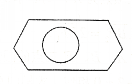 如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒芝麻(芝麻落到任何位置可能性相等),恰有27粒落入半径为1的圆内,则该多边形的面积约为( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com