
分析 (1)根据椭圆的性质列方程解出a2,b2;
(2)设C(2cosθ,$\sqrt{3}$sinθ),N(0,x),根据AN=CN,AN⊥CN列方程解出x即可.
解答 解:(1)∵椭圆E经过点P(1,$\frac{3}{2}$),且焦点为F(-1,0),
∴$\left\{\begin{array}{l}{\frac{1}{{a}^{2}}+\frac{9}{4{b}^{2}}=1}\\{{a}^{2}-{b}^{2}=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}^{2}=4}\\{{b}^{2}=3}\end{array}\right.$,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
(2)A(-2,0),设C(2cosθ,$\sqrt{3}$sinθ),N(0,x),则sinθ≠0.
∴AN2=4+x2,CN2=4cos2θ+($\sqrt{3}$sinθ-x)2,kAN=$\frac{x}{2}$,kCN=$\frac{\sqrt{3}sinθ-x}{2cosθ}$.
∵△ANC是以AC为斜边的等腰直角三角形,
∴AN=CN,即4+x2=4cos2θ+($\sqrt{3}$sinθ-x)2,
整理得sinθ+2$\sqrt{3}$x=0,∴x=-$\frac{sinθ}{2\sqrt{3}}$.
又AN⊥CN,即kAN•kCN=-1.
∴$\frac{x-\sqrt{3}sinθ}{2cosθ}=\frac{2}{x}$,即x2-$\sqrt{3}$x•sinθ=4cosθ,
把x=-$\frac{sinθ}{2\sqrt{3}}$代入上式得$\frac{7}{12}si{n}^{2}θ$=4cosθ,即7-7cos2θ=48cosθ,
解得cosθ=$\frac{1}{7}$,∴sinθ=±$\frac{4\sqrt{3}}{7}$.
∴x=±$\frac{2}{7}$.
∴C点坐标为(0,$\frac{2}{7}$)或(0,-$\frac{2}{7}$).
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-2≤x≤2} | B. | {x|x≥2} | C. | {x|0≤x≤2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\int_1^2{f(x)dx=28}$ | B. | $\int_2^3{f(x)dx=28}$ | ||
| C. | $\int_1^2{2f(x)dx=56}$ | D. | $\int_1^2{f(x)dx+}\int_2^3{f(x)dx=56}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 正三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等腰直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
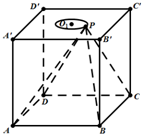 正方体ABCD-A1B1C1D1的棱长为6,半径为$\sqrt{6}$的圆O1在平面A1B1C1D1内,其圆心O1为正方形A1B1C1D1的中心,P为圆O1上的一个动点,则多面体PABCD的外接球的半径为$\sqrt{22}$.
正方体ABCD-A1B1C1D1的棱长为6,半径为$\sqrt{6}$的圆O1在平面A1B1C1D1内,其圆心O1为正方形A1B1C1D1的中心,P为圆O1上的一个动点,则多面体PABCD的外接球的半径为$\sqrt{22}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com