Question

【题目】函数f(x)＝aln x＋bx2图象上点P(1，f(1))处的切线方程为2x－y－3＝0.

(1)求函数f(x)的解析式及单调区间；

(2)若函数g(x)＝f(x)＋m－ln 4在上恰有两个零点，求实数m的取值范围．

Answer 1

【答案】（1）f′(x)＝＋2bx，f(x)的单调递增区间为(0， )，单调递减区间为(，＋∞)．（2）2<m≤4－2ln 2.

【解析】试题分析：（1）由导数的几何意义知切线的斜率为点P处导数，点P也在切线上，构造方程组可得函数的解析式，再由函数的解析式进行求导，判断导数大于零和小于零的区间，即函数的单调区间；（2）易知函数，令，分离变量，构造新的函数，对新函数求导判断函数的单调性，再求出新函数的端点值和极值，从而可得实数m的取值范围．

试题解析：∵切点在直线2x－y－3=0上，∴f（1）=－１．

,由已知得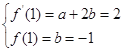a=4,b=-1.

∴．

∴单调增区间为（0，），减区间为[，+

（2）f（x）的定义域为. =4lnx-x2+m-ln4.

令g（x）="0," 得4lnx-x2+m-ln4.=0m=x2-4lnx+ln4．

记.则,

当时,,单调递减;

当时,,单调递增.

,.

由题意,．