
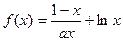
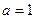 时,求
时,求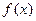 的单调区间;
的单调区间;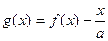 在区间
在区间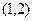 上不单调,求实数
上不单调,求实数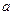 的取值范围.
的取值范围. 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:不详 题型:解答题
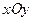 中,直线
中,直线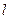 的参数方程为
的参数方程为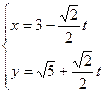 (
( 为参数),在极
为参数),在极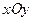 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以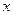 轴正半轴为极轴)中,圆C的方程为
轴正半轴为极轴)中,圆C的方程为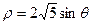 。
。 交于点A、B,若点P的坐标为
交于点A、B,若点P的坐标为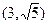 ,求|PA|+|PB|。
,求|PA|+|PB|。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
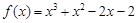 的一个正数零点附近的函数值用二分法计算,其参
的一个正数零点附近的函数值用二分法计算,其参| f (1) = -2 | f (1.5) = 0.625 | f (1.25) =" " -0.984 |
| f (1.375) =" " -0.260 | f (1.4375) = 0.162 | f (1.40625) = -0.054 |
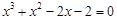 的一个近似根(精确到0.1)为
的一个近似根(精确到0.1)为查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
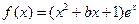 在
在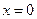 处切线斜率为-1.
处切线斜率为-1.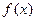 的解析式;
的解析式;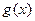 的定义域为
的定义域为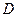 ,若存在区间
,若存在区间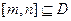 ,使得
,使得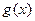 在
在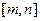 上的值域也是
上的值域也是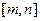 ,则称区间
,则称区间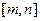 为函数
为函数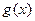 的“保值区间”
的“保值区间”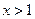 时,函数
时,函数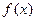 不存在“保值区间”;
不存在“保值区间”;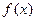 是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”(不必证明);若不存在,说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com