
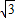 km处,河流沿岸曲线PQ上任意一点到公路l和到A地距离相等.现要在曲线PQ上一处建一座码头,向A、B两地运货物,经测算,从M到A、到B修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元.
km处,河流沿岸曲线PQ上任意一点到公路l和到A地距离相等.现要在曲线PQ上一处建一座码头,向A、B两地运货物,经测算,从M到A、到B修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元.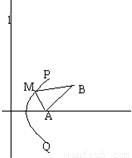
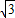 )a
)a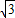 +1)a
+1)a科目:高中数学 来源: 题型:
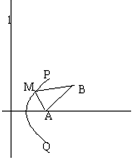 如图,南北方向的公路l,A地在公路正东2km处,B地在A东偏北300方向2
如图,南北方向的公路l,A地在公路正东2km处,B地在A东偏北300方向2| 3 |
查看答案和解析>>
科目:高中数学 来源:2008年高考数学模拟创新试题分类汇编(解析几何) 题型:013
如图,南北方向的公路l,A地在公路正东2 km处,B地在A东偏北30°方向2![]() km处,河流沿岸曲线PQ上任意一点到公路l和到A地距离相等.现要在曲线PQ上一处建一座码头,向AB两地运货物,经测算,从M到A到B修建费用都为a万元/km,那么,修建这条公路的总费用最低是________万元
km处,河流沿岸曲线PQ上任意一点到公路l和到A地距离相等.现要在曲线PQ上一处建一座码头,向AB两地运货物,经测算,从M到A到B修建费用都为a万元/km,那么,修建这条公路的总费用最低是________万元
A.(2+![]() )a
)a
B.2(![]() +1)a
+1)a
C.5a
D.6a
查看答案和解析>>
科目:高中数学 来源:全优设计选修数学-2-1苏教版 苏教版 题型:013
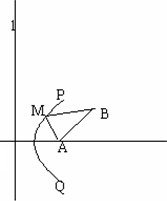
如图,南北方向的公路l,A地在公路的正东2 km处,B地在A地东偏北30°方向![]() km处,河流沿岸PQ(曲线)上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A,M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
km处,河流沿岸PQ(曲线)上任一点到公路l和到A地距离相等.现要在曲线PQ上选一处M建一座码头,向A、B两地转运货物,经测算从M到A,M到B修建公路的费用均为a万元/km,那么修建这两条公路的总费用最低是
(![]() )a万元
)a万元
2(![]() )a万元
)a万元
5a万元
6a万元
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建省高三上学期期末考练习三理科数学试卷(解析版) 题型:选择题
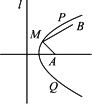
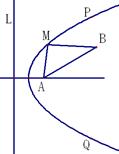
如图,南北方向的公路 ,A地在公路正东2 km处,B地在A东偏北300方向2
,A地在公路正东2 km处,B地在A东偏北300方向2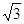 km处,河流沿岸曲线
km处,河流沿岸曲线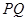 上任意一点到公路
上任意一点到公路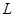 和到
和到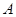 地距离相等.现要在曲线
地距离相等.现要在曲线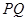 上一处建一座码头,向
上一处建一座码头,向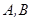 两地运货物,经测算,从
两地运货物,经测算,从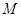 到
到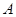 、到
、到 修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
修建费用都为a万元/km,那么,修建这条公路的总费用最低是( )万元
A.(2+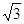 )a B.2(
)a B.2(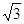 +1)a C.5a D.6ª
+1)a C.5a D.6ª
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com