
分析 由空间中直线与平面的位置关系结合线面角逐一判断(1)、(2)、(3)错误;画图分类证明(4)正确.
解答 解:对于(1),当n条斜线段与平面所成角不等时,斜线段长相等,它们在平面内的射影长不相等,故(1)错误;
对于(2),直线a、b不在平面α内,它们在平面α内的射影是两条平行直线,则a∥b或a与b异面,故(2)错误;
对于(3),与同一平面所成的角相等的两条直线位置关系有平行、相交或异面,故(3)错误;
对于(4),当直线在平面内或与平面平行时,直线与平面所成角为0°角,平面内所有直线与该直线所成角都大于等于0°;
当直线与平面垂直时,直线与平面所成角为90°,平面内所有直线与该直线所成角都等于90°;
当直线为平面的斜线OA时,如图,过A作AB⊥α,垂足为B,则直线与平面所成角为∠AOB=θ,
若平面内直线l与OB平行(或是OB),l与OA所成角为θ;
若l与OB不平行,平移直线l过O,过B作BC⊥l=C,连接AC,l与OA所成角为∠AOC,
∵sinθ=$\frac{AB}{OA}$,sin∠AOC=$\frac{AC}{OA}$,而AC>AB,∴sin∠AOC>sin∠θ,有∠AOC>∠θ,故(4)正确.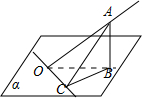
综上,正确命题的序号是(4).
故答案为:(4).
点评 本题考查命题的真假判断与应用,考查线面角,考查空间想象能力和思维能力,属中档题.


科目:高中数学 来源: 题型:选择题

| A. | 2$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p1+p2+p3 | B. | 1-(1-p1)(1-p2)(1-p3) | C. | 1-p1p2p3 | D. | p1p2p3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com