
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
本小题考查多项式函数的导数,函数极值的判定,二次函数与二次方程等基础知识的综合运用,考查用数形结合的数学思想分析问题,解决问题的能力.
(Ⅰ)解:f′(x)=ax2+2(a+d)x+a+2d=(x+1)(ax+a+2d).
令f′(x)=0,由a≠0得x=-1或x=-1-![]() .
.
∵a>0,d>0.
∴-1-![]() <-1.
<-1.
当-1-![]() <x<-1时,f′(x)<0,
<x<-1时,f′(x)<0,
当x>-1时,f′(x)>0.
所以f(x)在x=-1处取得极小值,即
x0=-1.
(Ⅱ)解:g(x)=ax2+(2a+4d)x+a+4d,
∵a>0,x∈R,
∴g(x)在x=-![]() =-1-
=-1-![]() 处取得极小值,即
处取得极小值,即
x1=-1-![]() .
.
由g(x)=0,即(ax+a+4d)(x+1)=0,
∵a>0,d>0,x2<x3,
∴x2=-1-![]() ,x3=-1.
,x3=-1.
∵f(x0)=f(-1)=-![]() a+(a+d)-(a+2d)+d=-
a+(a+d)-(a+2d)+d=-![]() a,
a,
g(x1)=g(-1-![]() )=a(-1-
)=a(-1-![]() )2+(2a+4d)(-1-
)2+(2a+4d)(-1-![]() )+a+4d=-
)+a+4d=-![]() ,
,
∴A(-1,-![]() a),B(-1-
a),B(-1-![]() ,-
,-![]() ),C(-1-
),C(-1-![]() ,0),D(-1,0).
,0),D(-1,0).
由四边形ABCD是梯形及BC与AD不平行,得AB∥CD.
∴-![]() ,即
,即
a2=12d2.
由四边形ABCD的面积为1,得![]() (|AB|+|CD|)·|AD|=1,即
(|AB|+|CD|)·|AD|=1,即
![]() (
(![]()
![]() )·
)·![]() =1,得
=1,得
d=1.
从而a2=12,得
a=2![]() .
.


科目:高中数学 来源: 题型:
(06年辽宁卷文)(12分)
已知函数![]() ,
,![]() ,其中
,其中![]() ,设
,设![]() 为
为![]() 的极小值点,
的极小值点,![]() 为
为![]() 的极值点,
的极值点,![]() ,并且
,并且![]() ,将点
,将点![]() 依次记为
依次记为![]() .
.
(1)求![]() 的值;
的值;
(2)若四边形![]() 为梯形且面积为1,求
为梯形且面积为1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三上学期月考数学试卷(解析版) 题型:解答题
已知函数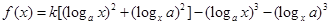 ,
,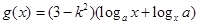 ,(其中
,(其中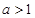 ),设
),设 .
.
(Ⅰ)当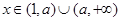 时,试将
时,试将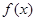 表示成
表示成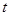 的函数
的函数 ,并探究函数
,并探究函数 是否有极值;
是否有极值;
(Ⅱ)当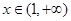 时,若存在
时,若存在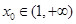 ,使
,使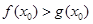 成立,试求
成立,试求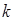 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源:2015届河北省石家庄市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知函数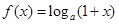 ,
,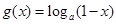 ,其中
,其中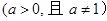 ,设
,设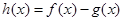 .
.
(1)求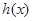 的定义域;
的定义域;
(2)判断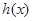 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(3)若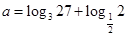 ,求使
,求使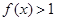 成立的
成立的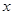 的集合.
的集合.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com