Question

在正方体ABCD-A₁B₁C₁D₁，棱长AA₁=2．
（1）E为棱CC₁的中点，求证：B₁D₁⊥AE；   
（2）求二面角C-AE-B的平面角的正切值．

Answer 1

分析：（1）连接A₁C₁，根据正方体的结构特征得到A₁C₁是AE在平面A₁C₁上的射影，进而根据三垂线定理得到B₁D₁⊥AE．
（2）连接BD交AC于O，过B点作BF⊥AE交AE于F，连接OF，可得∠BFO是二面角B-AE-C的平面角，根据相似三角形性质求出OF后，解三角形BOF即可，得到二面角B-AE-C的平面角

解答：证明：（1）连接A₁C₁，
∵AA₁⊥平面A₁C₁，
∴A₁C₁是AE在平面A₁C₁上的射影，
在正方形A₁B₁C₁D₁中，B₁D₁⊥A₁C₁
∴B₁D₁⊥AE
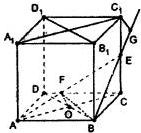
解：（2）连接BD交AC于O，过B点作BF⊥AE交AE于F，连接OF
∵EC⊥平面AC在正方形ABCD中，BD⊥AC，∴BD⊥平面ACE
∴OF是BF在平面EAC上的射影，∴AE⊥FO∴∠BFO是二面角B-AE-C的平面角
在正方形ABCD中，BO=AO=

1

2

AC=

2

在Rt△ACE中，AE=3，
∵△AOF∽△AEC，
∴

OA

OF

=

AE

EC

∴OF=

OA•EC

AE

=

2

3

在Rt△BOF中，tan∠BFO=

OB

OF

=3

点评：本题考查的知识点是二面角的平面角及求法，点到平面的距离，线线垂直的判定，其中（1）的关键是用三垂线定理证明线线垂直，（2）的关键是确定∠BFO是二面角B-AE-C的平面角．