函数y=ex-x+1,x∈[-1,2]的值域为________.
[2,e
2-1]
分析:求出函数的导数并且判断利用导数判断函数在定义域内的单调性,即可单调函数的最小值,再求出定义域的两个端点所对应的函数值,进行比较大小即可得到答案.
解答:由题意可得:函数y=e
x-x+1,
所以y′=e
x-1,
因为x∈[-1,2],
所以当x∈[-1,0]时y′=e
x-1<0,当x∈[0,2]时,y′=e
x-1>0,
所以函数的单调增区间为[0,2],减区间为[-1,0],
所以当x=0时函数有最小值2.
当x=-1时,y=2+

,当x=2时,y=e
2-1,显然
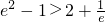
,
所以函数的最大值为e
2-1.
所以函数的值域为[2,e2-1].
故答案为[2,e
2-1].
点评:解决此类问题的关键是熟练掌握利用导数判断函数的单调性,进而求出函数的最值得到函数的值域.

 ,当x=2时,y=e2-1,显然
,当x=2时,y=e2-1,显然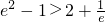 ,
,
