
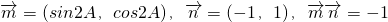 .
. 的夹角;
的夹角;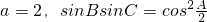 .求角B,C所对的边长b,c.
.求角B,C所对的边长b,c.
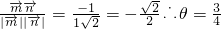 π
π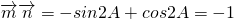
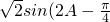 )=1
)=1 =
=
 ≤A<π
≤A<π π
π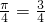 π
π
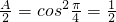
 -B)=1
-B)=1 ∴0<2B<π
∴0<2B<π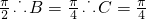
 且所对的边长a=2
且所对的边长a=2
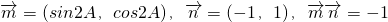 .代入向量夹角公式,即可求出向量
.代入向量夹角公式,即可求出向量 的夹角;
的夹角;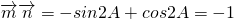 ,结合角A是△ABC的最大内角,我们易确定出A的大小,再由
,结合角A是△ABC的最大内角,我们易确定出A的大小,再由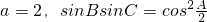 .结合诱导公式及二倍角公式,易求出三角形其它两个角的大小及两边长.
.结合诱导公式及二倍角公式,易求出三角形其它两个角的大小及两边长.

 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
| π |
| 2 |
| π |
| 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| 3 |
| a |
| b |
| π |
| 6ω |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
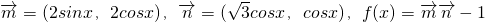 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间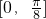 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年内蒙古乌兰察布市集宁一中高三(上)第六次周考数学试卷(解析版) 题型:解答题
 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市崇明县建设中学高三(下)摸底数学试卷(解析版) 题型:解答题
 .
. ,把所得到的图象再向左平移
,把所得到的图象再向左平移 单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com