
分析 四边形PAOB为2个对称的直角三角形构成,由OA与OB为圆的半径,其值固定不变,得到当PO最小值,四边形PAOB的面积最小,即圆心到直线的距离最小,利用点到直线的距离公式求出PO的长,利用勾股定理求出此时AP的长,利用三角形的面积公式求出两直角三角形的面积,即为四边形PAOB面积的最小值.
解答 解:由圆x2+y2=4,得到圆心O坐标为(0,0),半径r=2,
又直线x+y-4=0,
∴|PO|min=$\frac{4}{\sqrt{2}}$=2$\sqrt{2}$,又|OA|=2,
∴在Rt△AOP中,利用勾股定理得:|AP|=2,
则四边形PAOB面积的最小值S=2×$\frac{1}{2}$×|OA|×|AP|=4.
故答案为:4.
点评 此题考查了直线与圆方程的应用,涉及的知识有:圆的标准方程,点到直线的距离公式,勾股定理,以及三角形面积的求法,其中根据题意得到|PO|的最小时,Rt△APO面积最小是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{2}$ | B. | 4 | C. | $8\sqrt{2}$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若x≠0,则$x+\frac{1}{x}$≥2 | |
| B. | “实数a=1”是“直线x+ay=0与直线x-ay=0互相垂直”的充要条件 | |
| C. | 命题“?x>0,x2-x≤0”的否定是“?x>0,x2-x>0” | |
| D. | 命题“若-1<x<1,则x2<1”的否命题是“若x2≥1,则x≥1或x≤-1” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
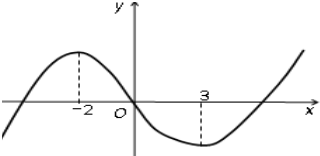
| A. | $({\frac{1}{2},+∞})$ | B. | $({-∞,\frac{1}{2}})$ | C. | (-2,3) | D. | (-∞,-2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-1)∪(\frac{1}{3},+∞)$ | B. | $(-∞,-2)∪(\frac{2}{3},+∞)$ | C. | $(-2,\frac{2}{3})$ | D. | $(-1,\frac{1}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
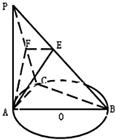 如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:
如图,PA垂直⊙O所在的平面,AB为⊙O的直径,C是⊙O上的一点,AE⊥PB与E,AF⊥PC于F,给出下列结论:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com