
(1)求数集序列第n个集合中最大数an的表达式;
(2)设数集序列第n个集合中各数之和为Tn.
①求Tn的表达式;
②令f(n)=(![]() )n,求证:2≤f(n)<3.
)n,求证:2≤f(n)<3.
解:(1)∵第n个集合有n个奇数,
∴在前n个集合中共有奇数的个数为1+2+3+…+(n-1)+n=![]() n(n+1).
n(n+1).
则第n个集合中最大的奇数an=2×![]() n(n+1)-1=n2+n-1.
n(n+1)-1=n2+n-1.
(2)①由(1)得an=n2+n-1,
从而得Tn=n(n2+n-1)-![]() ×2=n3.
×2=n3.
②由①得Tn=n3,
∴f(n)=(1+![]() )n=(1+
)n=(1+![]() )n(n∈N*).
)n(n∈N*).
ⅰ当n=1时,f(1)=2,显然2≤f(1)<3.
ⅱ当n≥2时,(1+![]() )n=
)n=![]() (
(![]() )0+
)0+![]() (
(![]() )1+
)1+![]() (
(![]() )2+…+
)2+…+![]() (
(![]() )n
)n
>![]() (
(![]() )0+
)0+![]() (
(![]() )1=2,
)1=2,
![]() (
(![]() )k=
)k=![]() ·
·![]() <
<![]()
≤![]() =
=![]() -
-![]() .
.
∴(1+![]() )n=
)n=![]() (
(![]() )0+
)0+![]() (
(![]() )1+
)1+![]() (
(![]() )2+…+
)2+…+![]() (
(![]() )n
)n
<1+1+(1-![]() )+(
)+(![]() -
-![]() )+…+(
)+…+(![]() -
-![]() )
)
=3-![]() <3,
<3,
即2<f(n)<3.
综上所述,2≤f(n)<3.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
| n |
 |
| i=1 |
| 1 | |||
|
| n-1 |
 |
| i=1 |
查看答案和解析>>
科目:高中数学 来源:2011年江苏省无锡市高考数学模拟试卷(2)(解析版) 题型:解答题
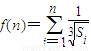 ,求证:
,求证: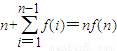 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com