[题目]对于三次函数f(x)＝ax3+bx2+cx+d(a≠0).给出定义:设f′(x)是函数y＝f(x)的导数.f″(x)是f′(x)的导数.若方程f″(x)＝0有实数解x0.则称点(x0.f(x0))为函数y＝f(x)的“拐点．某同学经过探究发现:任何一个三次函数都有对称中心.且“拐点就是对称中心．若.请你根据这一发现判断函数的对称中心为( )A 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】对于三次函数f(x)＝ax3＋bx2＋cx＋d(a≠0)，给出定义：设f′(x)是函数y＝f(x)的导数，f″(x)是f′(x)的导数，若方程f″(x)＝0有实数解x0，则称点(x0，f(x0))为函数y＝f(x)的“拐点”．某同学经过探究发现：任何一个三次函数都有对称中心，且“拐点”就是对称中心．若，请你根据这一发现判断函数的对称中心为(　　)

A. (，1) B. (－，1) C. (，－1) D. (－，－1)

【答案】A

【解析】依题意，得f′(x)＝x2－x＋3，∴f″(x)＝2x－1，

由f″(x)＝0，即2x－1＝0，得x＝，

又f()＝1，∴函数f(x)＝x3－x2＋3x－的对称中心为(，1)．

故选A.

练习册系列答案

黄冈经典阅读系列答案

文言文课外阅读特训系列答案

轻松阅读训练系列答案

南大教辅初中英语任务型阅读与首字母填空系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】曲线的参数方程为 (为参数)，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，直线的极坐标方程为.

(1)写出的直角坐标方程，并且用 (为直线的倾斜角，为参数)的形式写出直线的一个参数方程；

(2) 与是否相交，若相交求出两交点的距离，若不相交，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．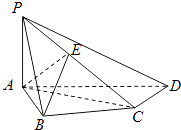

（1）证明CD⊥AE；
（2）证明PD⊥平面ABE；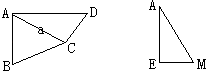

（3）求二面角A﹣PD﹣C的正切值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=log （3x2﹣ax+5）在[﹣1，+∞）上单调递减，则实数a的取值范围是（）
A.[﹣8，﹣6]
B.（﹣8，﹣6]
C.（﹣∞，﹣8）∪（﹣6，+∞）
D.（﹣∞，﹣6]

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某自来水厂的蓄水池存有400吨水，水厂每小时可向蓄水池中注水60吨，同时蓄水池又向居民小区不间断供水，t小时内供水总量为吨，（0≤t≤24）
（1）从供水开始到第几小时时，蓄水池中的存水量最少？最少水量是多少吨？
（2）若蓄水池中水量少于80吨时，就会出现供水紧张现象，请问：在一天的24小时内，有几小时出现供水紧张现象．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知F1 ， F2为椭圆C：（a＞b＞0）的左、右焦点，M为椭圆C的上顶点，且|MF1|=2，右焦点与右顶点的距离为1．
（1）求椭圆C的标准方程；
（2）若直线l与椭圆C相交于A，B两点，且直线OA，OB的斜率kOA ， kOB满足kOAkOB=﹣ ，求△AOB的面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知定义在[﹣2，2]上的函数y=f（x）和y=g（x），其图象如图所示：给出下列四个命题：
①方程f[g（x）]=0有且仅有6个根 ②方程g[f（x）]=0有且仅有3个根
③方程f[f（x）]=0有且仅有5个根 ④方程g[g（x）]=0有且仅有4个根
其中正确命题的序号（）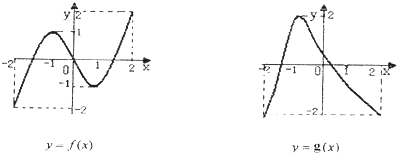

A.①②③
B.②③④
C.①②④
D.①③④