
【题目】用反证法证明:已知a,b均为有理数,且 ![]() 和
和 ![]() 都是无理数,求证:
都是无理数,求证: ![]() 是无理数.
是无理数.
【答案】【解答】
证明:证法一:假设 ![]() 为有理数,令
为有理数,令 ![]() =t ,
=t ,
则![]() ,两边平方,得
,两边平方,得![]() ,
,
∴![]() .
.
∵a , b , t均为有理数,∴![]() 也是有理数.
也是有理数.
即 ![]() 为有理数,这与已知
为有理数,这与已知 ![]() 为无理数矛盾.
为无理数矛盾.
∴ ![]() 一定是无理数.
一定是无理数.
证法二:假设 ![]() 为有理数,
为有理数,
则![]() .
.
由 a>0.b>0 ,得![]() .
.
∴![]() .
.
∵a , b为有理数,且 ![]() 为有理数,
为有理数,
∴ ![]() 为有理数,即
为有理数,即 ![]() 为有理数.
为有理数.
∴![]() 为有理数,即 2
为有理数,即 2![]() 为有理数.
为有理数.
从而 ![]() 也应为有理数,这与已知
也应为有理数,这与已知 ![]() 为无理数矛盾,
为无理数矛盾,
∴ ![]() 一定是无理数.
一定是无理数.
【解析】本题主要考查了反证法与放缩法,解决问题的关键是按反证法的步骤,即先否定结论,把假设和已知结合起来,推出矛盾,即假设不成立;结论为肯定形式或者否定形式的命题的证明常用反证法,通过反设将肯定命题转化为否定命题或将否定命题转化为肯定命题,然后用转化后的命题作为条件进行推理,很一般推出矛盾,从而达到证题的目的.
【考点精析】掌握反证法与放缩法是解答本题的根本,需要知道常见不等式的放缩方法:①舍去或加上一些项②将分子或分母放大(缩小).


科目:高中数学 来源: 题型:
【题目】已知向量 ![]() ,
, ![]() ,设函数
,设函数 ![]() .
.
(1)求函数 ![]() 的单调递增区间;
的单调递增区间;
(2)在 ![]() 中,边
中,边 ![]() 分别是角
分别是角 ![]() 的对边,角
的对边,角 ![]() 为锐角,若
为锐角,若![]() ,
, ![]() ,
, ![]() 的面积为
的面积为 ![]() ,求边
,求边 ![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,三棱锥V﹣ABC中,VA=VB=AC=BC=2,AB=2 ![]() ,VC=1,线段AB的中点为D.
,VC=1,线段AB的中点为D.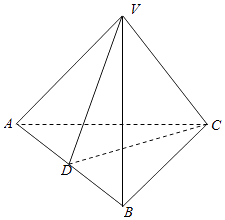
(1)求证:平面VCD⊥平面ABC;
(2)求三棱锥V﹣ABC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{an}的前n项和,Sn=2n2+5n.
(1)求证:数列{3 ![]() }为等比数列;
}为等比数列;
(2)设bn=2Sn﹣3n,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn为数列{cn}的前n项和,an=2n , bn=50﹣3n,cn= ![]() .
.
(1)求c4与c8的等差中项;
(2)当n>5时,设数列{Sn}的前n项和为Tn .
(ⅰ)求Tn;
(ⅱ)当n>5时,判断数列{Tn﹣34ln}的单调性.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com