
【题目】如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上. 
(1)求证:平面ACD⊥平面ABD;
(2)求二面角G﹣AC﹣D的平面角的余弦值.
【答案】
(1)解:在等腰梯形ABCD中,∵AD∥BC,AD=CD=AB,∠ABC=60°,∴∠BAD=120°,从而∠ABD=∠ADB=30°,可得∠BDC=90°,
在三棱锥A﹣BCD中,∵点A在平面BCD上的投影G落在BD上,∴AG⊥BD,于是G为BD中点.
∵  ∴CD⊥面ABD,又CD面ADC,∴平面ACD⊥平面ABD
∴CD⊥面ABD,又CD面ADC,∴平面ACD⊥平面ABD
(2)解:由(1)得AG⊥面BCD,且G为BD中点,CD⊥面ABD,
取BC中点M,则MG∥CD,于是以G为原点,建立如图的空间直角坐标系G﹣xyz,
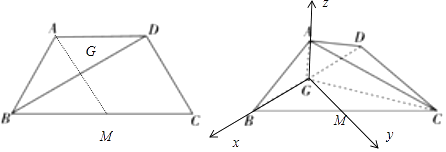
设AB=1,则BD= ![]() ,BC=2,CD=1,于是A(0,0,
,BC=2,CD=1,于是A(0,0, ![]() ),B(
),B( ![]() ,0,0).,C(﹣
,0,0).,C(﹣ ![]() ,1,0),D(﹣
,1,0),D(﹣ ![]() ,0,0)
,0,0)
![]() ,
, ![]() .
.
设面AGC的法向量为 ![]() ,由
,由  ,取
,取 ![]() ,
,
设面ADC的法向量为 ![]() ,由
,由 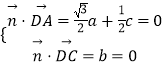 ,取
,取 ![]()
cos< ![]() ,
, ![]() >=
>= ![]() .
.
二面角G﹣AC﹣D的平面角的余弦值为 ![]()
【解析】(1)在等腰梯形ABCD中,可得∠ABD=∠ADB=30°,∠BDC=90°,在三棱锥A﹣BCD中,由点A在平面BCD上的投影G落在BD上,得CD⊥面ABD,又CD面ADC,即平面ACD⊥平面ABD;(2)取BC中点M,则MG∥CD,于是以G为原点,建立如图的空间直角坐标系G﹣xyz,设AB=1,则BD= ![]() ,BC=2,CD=1,于是A(0,0,
,BC=2,CD=1,于是A(0,0, ![]() ),B(
),B( ![]() ,0,0),C(﹣
,0,0),C(﹣ ![]() ,1,0),D(﹣
,1,0),D(﹣ ![]() ,0,0),利用法向量求解.
,0,0),利用法向量求解.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=blnx,g(x)=ax2﹣x(a∈R).
(1)若曲线f(x)与g(x)在公共点A(1,0)处有相同的切线,求实数a、b的值;
(2)在(1)的条件下,证明f(x)≤g(x)在(0,+∞)上恒成立;
(3)若a=1,b>2e,求方程f(x)﹣g(x)=x在区间(1,eb)内实根的个数(e为自然对数的底数).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学巨著,内容极为丰富,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等,问各得几何.”意思是:“5人分取5钱,各人所得钱数依次成等差数列,其中前2人所得钱数之和与后3人所得钱数之和相等.”,则其中分得钱数最多的是( )
A.![]() 钱
钱
B.1钱
C.![]() 钱
钱
D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面是以O为中心的菱形,
中,底面是以O为中心的菱形,![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,M为BC上一点.
,M为BC上一点.
![]() 当BM等于多少时,
当BM等于多少时,![]() 平面POM?
平面POM?
![]() 在满足
在满足![]() 的条件下,若
的条件下,若![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】去年“十一”期间,昆曲高速公路车辆较多.某调查公司在曲靖收费站从7座以下小型汽车中按进收费站的先后顺序,每间隔50辆就抽取一辆的抽样方法抽取40辆汽车进行抽样调查,将他们在某段高速公路的车速(![]() )分成六段:
)分成六段:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 后,得到如图的频率分布直方图.
后,得到如图的频率分布直方图.
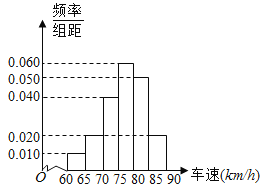
(I)调查公司在抽样时用到的是哪种抽样方法?
(II)求这40辆小型汽车车速的众数和中位数的估计值;
(III)若从这40辆车速在![]() 的小型汽车中任意抽取2辆,求抽出的2辆车车速都在
的小型汽车中任意抽取2辆,求抽出的2辆车车速都在![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图. (Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.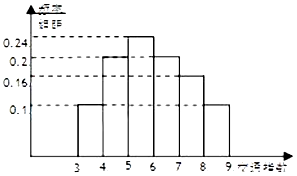
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com