
分析 (1)根据函数奇偶性的定义进行证明即可.
(2)根据f(x)与反函数的单调性相同,根据最小值建立方程关系求出a的值进行求解即可.
解答 解:(1)当a=-$\frac{1}{2}$时,$f(x)=-\frac{1}{2}x+{log_2}({2^x}+1)$,定义域为R,
$f(-x)=\frac{1}{2}x+{log_2}({2^{-x}}+1)$=$\frac{1}{2}x+{log_2}(\frac{{1+{2^x}}}{2^x})$
=$\frac{1}{2}x+{log_2}({2^x}+1)-{log_2}{2^x}$=$-\frac{1}{2}x+{log_2}({2^x}+1)$=f(x),
∴函数f(x)是偶函数.
(2)∵函数f(x)与f-1(x)单调性相同,
∴当a>0时,函数f(x)为增函数,
则y=f(x)+f-1(x)在区间[1,2]上为增函数,
则函数的最小值为当x=1时,y=f(1)+f-1(1)=1+log23,
即a+log23+f-1(1)=1+log23,则f-1(1)=1-a,
即f(1-a)=1,
则a(1-a)+log2(21-a+1)=1,
得a=1,
此时f(x)=x+log2(2x+1)在[1,2]上是增函数,
则函数的最大值为f(2)=2+log2(22+1)=2+log25.
点评 本题主要考查函数奇偶性的判断以及函数单调性的应用,根据函数与反函数的单调性相同建立方程求出a的值是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 114 | B. | 10 | C. | 150 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
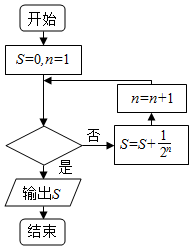
| A. | n≥12? | B. | n≥11? | C. | n≥10? | D. | n≥9? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com