
分析 (1)运用分段函数的形式,顾客购物全额x与应付金额y之间的函数关系,并画出流程图;
(2)由300×0.9=270<282.2,则该顾客购物全额超过300元,运用第三段函数式,令y=282.8,解出x.
解答 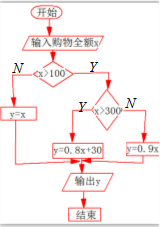 解:(1)顾客购物全额x与应付金额y之间的函数关系如下
解:(1)顾客购物全额x与应付金额y之间的函数关系如下
y=$\left\{\begin{array}{l}{x,0<x≤100}\\{0.9x,100<x≤300}\\{0.9×300+0.8(x-300),x>300}\end{array}\right.$,
流程图如右:
(2)设顾客的购物全额为x,则
由300×0.9=270<282.2,
则该顾客购物全额超过300元,
由y=300×0.9+0.8(x-300)=282.8,
解得x=316,
所以顾客的购物全额为316元.
点评 本题考查分段函数和运用,同时考查流程图的画法,属于基础题.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪($\frac{1+\sqrt{3}}{2}$,+∞) | B. | (-∞,$\frac{-1+\sqrt{3}}{2}$)∪(1,+∞) | ||
| C. | (-∞,-1)∪(1,+∞) | D. | (-∞,$\frac{-1-\sqrt{3}}{2}$)∪($\frac{1+\sqrt{3}}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{36}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{21}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
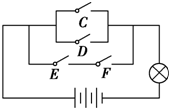 一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )
一个电路如图所示,C、D、E、F为4个开关,其闭合的概率都是$\frac{1}{2}$,且是相互独立的,则灯亮的概率是( )| A. | $\frac{9}{16}$ | B. | $\frac{7}{16}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com