
已知数列{an}的前n项和Sn=a[2-( )n-1]-b[2-(n+1)(
)n-1]-b[2-(n+1)( )n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得( )
)n-1](n=1,2,…),其中a,b是非零常数,则存在数列{xn}、{yn}使得( )
A.an=xn+yn,其中{xn}为等差数列,{yn}为等比数列
B.an=xn+yn,其中{xn}和{yn}都为等差数列
C.an=xn·yn,其中{xn}为等差数列,{yn}为等比数列
D.an=xn·yn,其中{xn}和{yn}都为等比数列
科目:高中数学 来源: 题型:
已知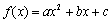 (a≠0),且方程
(a≠0),且方程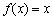 无实根。现有四个命题①若
无实根。现有四个命题①若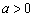 ,则不等式
,则不等式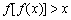 对一切
对一切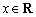 成立;②若
成立;②若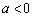 ,则必存在实数
,则必存在实数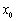 使不等式
使不等式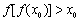 成立;③方程
成立;③方程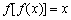 一定没有实数根;④若
一定没有实数根;④若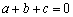 ,则不等式
,则不等式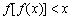 对一切
对一切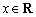 成立。其中真命题的个数是 ( )
成立。其中真命题的个数是 ( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
若不等式 3x2-logax<0的解集为{x|0<x<
3x2-logax<0的解集为{x|0<x<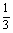 =的非空子集,则实数a的取值范围是 ( )
=的非空子集,则实数a的取值范围是 ( )
A.[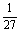 ,1] B.(
,1] B.(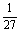 ,1)
,1)
C.(0,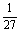 ) D.(0,
) D.(0,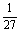 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}的各项都是正数,且满足:a0=1,an+1= an·(4-an),n
an·(4-an),n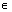 N.
N.
(1)证明an<an+1<2,n∈N.
(2)求数列{an}的通项公式an.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直线l1:y=kx+1-k(k≠0,k≠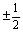 )与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.
)与l2相交于点P.直线l1与x轴交于点P1,过点P1作x轴的垂线交于直线l2于点Q1,过点Q1作y轴的垂线交直线l1于点P2,过点P2作x轴的垂线交直线l2于点Q2,…这样一直作下去,可得到一系列点P1,Q1,P2,Q2,…点Pn(n=1,2,…)的横坐标构成数列{xn}.
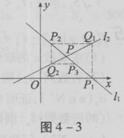
(Ⅰ)证明xn+1-1=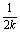 (xn-1),(n∈N*);
(xn-1),(n∈N*);
(Ⅱ)求数列{xn}的通项公式;
(Ⅲ)比较2|PPn|2与4k2|PP1|2+5的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知无穷等比数列{an}的各项和为 ,则a1的范围是 ( )
,则a1的范围是 ( )
A.-1<a1<1
B.0<a1<1
c.0<a1< 或
或 <a1<1
<a1<1
D.所给条件不足以确定a1,的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
计算机是将信息转换成二进制数进行处理的,二进制即“逢二进一”,如(1101)2,表示二进制数,将它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数(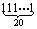 )2转换成十进制数是 .
)2转换成十进制数是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知抛物线 的焦点为
的焦点为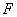 ,顶点为
,顶点为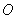 ,准线为
,准线为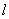 ,过该抛物线上异于顶点
,过该抛物线上异于顶点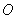 的任意一点
的任意一点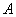 作
作 于点
于点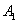 ,以线段
,以线段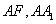 为邻边作平行四边形
为邻边作平行四边形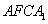 ,连接直线
,连接直线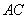 交
交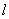 于点
于点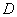 ,延长
,延长 交抛物线于另一点
交抛物线于另一点 。若
。若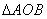 的面积为
的面积为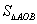 ,
,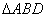 的面积为
的面积为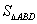 ,则
,则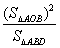 的最大值为____________。
的最大值为____________。
查看答案和解析>>
科目:高中数学 来源: 题型:
双曲线x2-y2=1的左焦点为F,点P为左支下半支上任意一点(异于顶点),则直线PF的斜率的变化范围是
A.(-∞,0) B.(1,+∞)C.(-∞,0)∪(1,+∞) D.(-∞,-1)∪(1,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com