


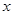 ��Ԫ��A��Ʒ������Ϊ
��Ԫ��A��Ʒ������Ϊ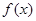 ��Ԫ��B��Ʒ������Ϊ
��Ԫ��B��Ʒ������Ϊ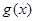 ��Ԫ��
��Ԫ��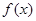 =
=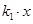 ��
��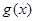 =
=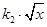 ����ͼ֪
����ͼ֪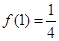
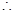
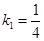 ����
����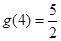
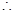
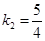
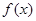 =
=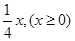 ��
��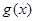 =
=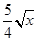 ��
��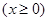 ����������6��
����������6��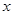 ��Ԫ����B��ƷͶ��10-
��Ԫ����B��ƷͶ��10-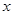 ��Ԫ������ҵ������Ϊy��Ԫ
��Ԫ������ҵ������Ϊy��Ԫ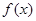 +
+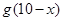 =
=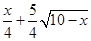 ����
����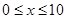 ����
���� 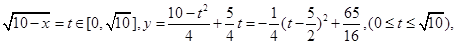
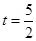 ��
��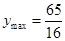 ����ʱ
����ʱ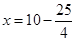 =3.75
=3.75 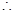 ��A��ƷͶ��3.75��Ԫ��B��ƷͶ��6.25��Ԫʱ��
��A��ƷͶ��3.75��Ԫ��B��ƷͶ��6.25��Ԫʱ��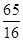 ��Ԫ. ����������14��
��Ԫ. ����������14��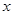 ��Ԫ��A��Ʒ������Ϊ
��Ԫ��A��Ʒ������Ϊ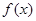 ��Ԫ��B��Ʒ������Ϊ
��Ԫ��B��Ʒ������Ϊ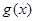 ��Ԫ��
��Ԫ��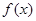 =
=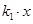 ��
��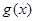 =
=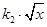 ����ͼ֪
����ͼ֪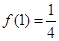 ��
��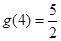 ,�ݴ˿ɵ�k1,k2��ֵ��ȷ��f(x),g(x)�Ľ���ʽ.
,�ݴ˿ɵ�k1,k2��ֵ��ȷ��f(x),g(x)�Ľ���ʽ.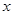 ��Ԫ����B��ƷͶ��10-
��Ԫ����B��ƷͶ��10-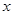 ��Ԫ������ҵ������Ϊy��Ԫ
��Ԫ������ҵ������Ϊy��Ԫ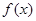 +
+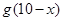 =
=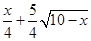 ����
����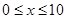 ����Ȼ����û�Ԫ��ת��Ϊ���κ��������������������������
����Ȼ����û�Ԫ��ת��Ϊ���κ��������������������������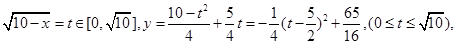


 �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
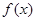 �ĵ�����
�ĵ�����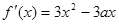 ��
��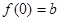 ��
��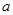 ��
��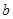 Ϊʵ����
Ϊʵ����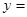
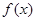 �ڵ㣨
�ڵ㣨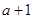 ��
��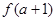 �������ߵ�б��Ϊ12����
�������ߵ�б��Ϊ12����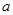 ��ֵ��
��ֵ��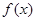 �������-1��1���ϵ���Сֵ�����ֵ�ֱ�Ϊ-2��1����
�������-1��1���ϵ���Сֵ�����ֵ�ֱ�Ϊ-2��1���� ������
������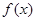 �Ľ���ʽ��
�Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �غ�
�غ� ��ͬʱ����������ͼ�����ؼ�ͷ����������ֱ������ǰ�������������г����ٶȷֱ���10��/���5��/�룬��֪
��ͬʱ����������ͼ�����ؼ�ͷ����������ֱ������ǰ�������������г����ٶȷֱ���10��/���5��/�룬��֪ ��.����������
��.���������� �ؼ�ֹͣ��
�ؼ�ֹͣ�� �����������
����������� �����������
�����������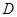 ������
������ �����Ϊ
�����Ϊ ����д��
����� ����
���� �ĺ�����ϵʽ�������䶨����.
�ĺ�����ϵʽ�������䶨����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
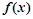 ��
��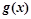 �Ƕ�����ͬһ����[a, b]�ϵ�����������������
�Ƕ�����ͬһ����[a, b]�ϵ�����������������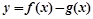 ��
��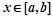 ����������ͬ����㣬���
����������ͬ����㣬���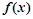 ��
��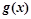 ��[a, b]���ǡ���ϵ������������[a, b]��Ϊ����ϵ���䡱����
��[a, b]���ǡ���ϵ������������[a, b]��Ϊ����ϵ���䡱����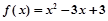 ��
��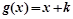 ��[0,3]���ǡ���ϵ����������k��ȡֵ��ΧΪ ( )
��[0,3]���ǡ���ϵ����������k��ȡֵ��ΧΪ ( )A��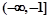 | B��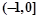 | C��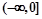 | D��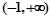 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
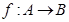 �������
�������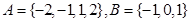 ��������
��������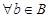 ������
������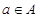 ʹ��
ʹ��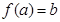 �������Ƹ�ӳ��Ϊ�Ӽ���
�������Ƹ�ӳ��Ϊ�Ӽ���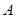 ������
������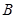 ��һ�������䡱����Ӽ���
��һ�������䡱����Ӽ���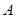 ������
������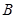 ���Խ������� ���������䡱��
���Խ������� ���������䡱��| A��18 | B��36 | C��64 | D��81 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
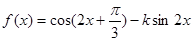 ����
����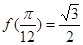 .
.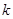 ��ֵ��
��ֵ��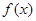 �ĵ����������估���ֵ����ָ��ȡ�����ֵʱ��
�ĵ����������估���ֵ����ָ��ȡ�����ֵʱ��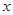 ֵ.
ֵ. �鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com