
科目:高中数学 来源: 题型:
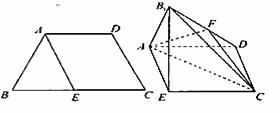
)已知四边形ABCD满足AD∥BC,BA=AD=DC=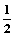 BC=a,E是BC的中点,将△BAE沿AE折起到
BC=a,E是BC的中点,将△BAE沿AE折起到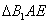 的位置,使平面
的位置,使平面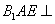 平面
平面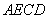 ,F为B1D的中点.
,F为B1D的中点.
(Ⅰ)证明:B1E∥平面ACF;
(Ⅱ)求平面ADB1与平面ECB1所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ex﹣mx+1的图象为曲线C,若曲线C存在与直线y=ex垂直的切线,则实数m的取值范围是( ).
A.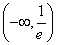 B. (
B. (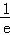 ,+∞) C.
,+∞) C. 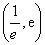 D.
D. 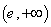
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,SA⊥平面ABC,AB ⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
⊥BC,过A作SB的垂线,垂足为E,过E作SC的垂线,垂足为F.
求证:AF⊥SC.
证明:要证AF⊥SC,只需证SC⊥平 面AEF,只需证AE⊥SC(因为______),只需证______,只需证AE
面AEF,只需证AE⊥SC(因为______),只需证______,只需证AE ⊥BC(因为________),只需证BC⊥平面SAB,只
⊥BC(因为________),只需证BC⊥平面SAB,只 需证BC⊥SA(因为______).由SA⊥平面ABC可知,上式成立.
需证BC⊥SA(因为______).由SA⊥平面ABC可知,上式成立.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com