
 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是A1B1、CC1的中点,过D1、E、F作平面D1EGF交BB1于G.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是A1B1、CC1的中点,过D1、E、F作平面D1EGF交BB1于G.分析 (1)通过平面ABB1A1∥平面DCC1D1.利用平面与平面平行的性质定理证明EG∥D1F.
(2)以D为原点分别以DA、DC、DD1为x轴、y轴、z轴,建立空间直角坐标系,求出平面D1EGF的法向量,平面C1D1E的法向,利用向量的数量积求解锐二面角C1-D1E-F的余弦值.
解答 解:(1)证明:在正方体ABCD-A1B1C1D1中,∵平面ABB1A1∥平面DCC1D1.
平面D1EGF∩平面ABB1A1=EG,
平面D1EGF∩平面DCC1D1=D1F,∴EG∥D1F.(4分)
(2)解:如图,以D为原点分别以DA、DC、DD1为x轴、y轴、z轴,建立空间直角坐标系,
则有D1(0,0,2),E(2,1,2),F(0,2,1),∴$\overrightarrow{{D_1}E}=(2,1,0),\overrightarrow{{D_1}F}=(0,2,-1)$(6分)
设平面D1EGF的法向量为$\overrightarrow{n}$=(x,y,z)
则由$\overrightarrow{n}•\overrightarrow{{D}_{1}E}=0$,$\overrightarrow{n}•\overrightarrow{{D}_{1}F}=0$
得$\left\{\begin{array}{l}2x+y=0\\ 2y-z=0\end{array}\right.$
取x=1,得y=-2,z=-4,所以$\overrightarrow{n}$=(1,-2,-4)(8分)
又平面C1D1E的法向为$\overrightarrow{D{D_1}}=(0,0,2)$(9分)
所以,cos$<\overrightarrow{n},\overrightarrow{D{D}_{1}}>$=$\frac{\overrightarrow{n}•\overrightarrow{D{D}_{1}}}{|\overrightarrow{n}||\overrightarrow{D{D}_{1}}|}$=$\frac{0×1+0×(-2)+2×(-4)}{2×\sqrt{{1}^{2}+(=2)^{2}+(-4)^{2}}}$=-$\frac{4\sqrt{21}}{21}$
所以,锐二面角C1-D1E-F的余弦值为$\frac{{4\sqrt{21}}}{21}$.(12分)
点评 本题考查平面与平面平行的性质定理,二面角的平面镜的求法,考查空间想象能力以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
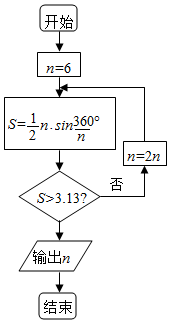 公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,如圆是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin15°=0.2588,sin7.50=0.1305.
公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,如圆是利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )(参考数据:sin15°=0.2588,sin7.50=0.1305.| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{4}$] | B. | (-∞,$\frac{1}{8}$] | C. | (0,$\frac{1}{4}$] | D. | (0,$\frac{1}{8}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com