Question

如图，四棱锥S—ABCD的底面ABCD是正方形，SA⊥平面ABCD，E是SC上一点.?

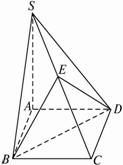
（1）求证：平面EBD⊥平面SAC；?

（2）假设SA=4，AB=2，求点A到平面SBD的距离；?

（3）当的值为多少时，二面角B-SC-D的大小为120°?

Answer 1

提示：（1）易证SA⊥BD、AC⊥BDBD⊥面SAC，得面EBD⊥面SAC.?

（2）用等体积法，易求出距离为.?

（3）分别以AB、AD、AS所在直线为x、y、z轴建立空间直角坐标系，不妨设AB=1，SA=h.

则B（1，0，0），D（0，1，0），C（1，1，0），S（0，0，h），不妨使EB⊥SC，设=λ(0＜λ＜1),则=λ(-1,-1,h).?

∴=(-λ,1-λ,λh).?

又·=λ-1+λ+λh²=0λh²=1-2λ,这时=（1-λ，-λ，λh）.?

而·=-1+λ+λ+λh²=0,?

∴DE⊥CS.?

由EB⊥SC,∴SC⊥面BED.?

∴∠BED是二面角BSCD的大小.∴∠BED=120°,且||=||=.?

这时， cos120°.?

∴λ(λ-1)+(λ-1)·λ+λ²h²?

=-［λ²+(1-λ)²+λ²h²］.?

∴6λ²-6λ+1+3λ²h²=0.?

又∵λh²=1-2λ(0＜λ＜1),?

∴λ=.?

这时，h²=1,即h=1.?

故=1时，二面角B-SC-D的大小为120°.