
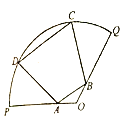
【题目】为丰富市民的文化生活,市政府计划在一块半径为200m,圆心角为![]() 的扇形地上建造市民广场,规划设计如图:内接梯形
的扇形地上建造市民广场,规划设计如图:内接梯形![]() 区域为运动休闲区,其中A,B分别在半径
区域为运动休闲区,其中A,B分别在半径![]() ,
,![]() 上,C,D在圆弧
上,C,D在圆弧![]() 上,
上,
![]() ;上,
;上,![]() ;
;![]() 区域为文化展区,
区域为文化展区,![]() 长为
长为![]() ,其余空地为绿化区域,且
,其余空地为绿化区域,且![]() 长不得超过200m.
长不得超过200m.
(1)试确定A,B的位置,使![]() 的周长最大?
的周长最大?
(2)当![]() 的周长最长时,设
的周长最长时,设![]() ,试将运动休闲区
,试将运动休闲区![]() 的面积S表示为
的面积S表示为![]() 的函数,并求出S的最大值.
的函数,并求出S的最大值.
【答案】(1)![]() 、
、![]() 都为50m;(2)
都为50m;(2)![]() ;
;![]() ;最大值为
;最大值为![]() .
.
【解析】
对于(1),设![]() ,
,![]() ,m,
,m,![]() ,在△OAB中,利用余弦定理可得
,在△OAB中,利用余弦定理可得![]() ,整理得
,整理得![]() ,结合基本不等式即可得出结论;
,结合基本不等式即可得出结论;
对于(2),当△AOB的周长最大时,梯形ACBD为等腰梯形,过O作OF⊥CD交CD于F,交AB于E,则E、F分别为AB,CD的中点,利用已知可表示出相关线段;然后利用梯形的面积公式可知,![]() ,
,![]() ,令
,令![]() ,
,![]() ,,结合导数,确定函数的单调性,即可求出S的最大值。
,,结合导数,确定函数的单调性,即可求出S的最大值。
解:(1)设![]() ,
,![]() ,m,
,m,![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() .
.
所以![]() .
.
所以![]() ,当且仅当
,当且仅当![]() 时,
时,![]() 取得最大值,
取得最大值,
此时![]() 周长取得最大值.
周长取得最大值.
答:当![]() 、
、![]() 都为50m时,
都为50m时,![]() 的周长最大.
的周长最大.
(2)当![]() 的周长最大时,梯形
的周长最大时,梯形![]() 为等腰梯形.
为等腰梯形.
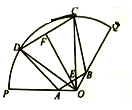
如上图所示,过O作![]() 交
交![]() 于F,交
于F,交![]() 于E,则E、F分别为
于E,则E、F分别为![]() 、
、![]() 的中点,
的中点,
所以![]() .由
.由![]() ,得
,得![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
又在![]() 中,
中,![]() ,故
,故![]() .
.
所以![]()
![]()
![]() ,
,![]() .
.
令![]() ,
,![]() ,
,
![]() ,
,![]() .
.
又![]() 及
及![]() 在
在![]() 上均为单调递减函数,
上均为单调递减函数,
故![]() 在
在![]() 上为单调递减函数.
上为单调递减函数.
因 ,故
,故![]() 在
在![]() 上恒成立,
上恒成立,
于是,![]() 在
在![]() 上为单调递增函数.
上为单调递增函数.
所以当![]() 时,
时,![]() 有最大值,此时S有最大值为
有最大值,此时S有最大值为![]() .
.
答:当![]() 时,梯形
时,梯形![]() 面积有最大值,且最大值为
面积有最大值,且最大值为![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】供电部门对某社区![]() 位居民2017年12月份人均用电情况进行统计后,按人均用电量分为
位居民2017年12月份人均用电情况进行统计后,按人均用电量分为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五组,整理得到如下的频率分布直方图,则下列说法错误的是
五组,整理得到如下的频率分布直方图,则下列说法错误的是

A. ![]() 月份人均用电量人数最多的一组有
月份人均用电量人数最多的一组有![]() 人
人
B. ![]() 月份人均用电量不低于
月份人均用电量不低于![]() 度的有
度的有![]() 人
人
C. ![]() 月份人均用电量为
月份人均用电量为![]() 度
度
D. 在这![]() 位居民中任选
位居民中任选![]() 位协助收费,选到的居民用电量在
位协助收费,选到的居民用电量在![]() 一组的概率为
一组的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某班级50名学生订阅数学、语文、英语学习资料的情况,其中A表示订阅数学学习资料的学生,B表示订阅语文学习资料的学生,C表示订阅英语学习资料的学生

(1)从这个班任意选择一名学生,用自然语言描述1,4,5,8各区域所代表的事件;
(2)用A,B,C表示下列事件:
①恰好订阅一种学习资料;
②没有订阅任何学习资料.
查看答案和解析>>
科目:高中数学 来源: 题型:
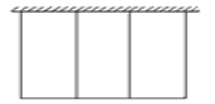
【题目】有一批材料可以建成200m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形,如何设计这块矩形场地的长和宽,能使面积最大,并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
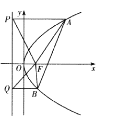
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上
上![]() 两点,在抛物线的准线上的射影分别为
两点,在抛物线的准线上的射影分别为![]() .
.
(1)如图,若![]() 点在线段
点在线段![]() 上,过
上,过![]() 作
作![]() 的平行线
的平行线![]() 与抛物线准线交于
与抛物线准线交于![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
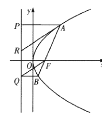
(2)如图,若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,OA,OB是两条互相垂直的笔直公路,半径OA=2km的扇形AOB是某地的一名胜古迹区域.当地政府为了缓解该古迹周围的交通压力,欲在圆弧AB上新增一个入口P(点P不与A,B重合),并新建两条都与圆弧AB相切的笔直公路MB,MN,切点分别是B,P.当新建的两条公路总长最小时,投资费用最低.设∠POA=![]() ,公路MB,MN的总长为
,公路MB,MN的总长为![]() .
.

(1)求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域;
的函数关系式,并写出函数的定义域;
(2)当![]() 为何值时,投资费用最低?并求出
为何值时,投资费用最低?并求出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com