
【题目】已知函数![]() (
(![]() ).
).
(Ⅰ)若![]() 在
在![]() 处的切线过点
处的切线过点![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 恰有两个极值点
恰有两个极值点![]() ,
,![]() (
(![]() ).
).
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)求证:![]() .
.
【答案】(Ⅰ) ![]() (Ⅱ) (ⅰ)
(Ⅱ) (ⅰ) ![]() (ⅱ)见证明
(ⅱ)见证明
【解析】
(Ⅰ)对函数进行求导,然后求出在![]() 处的切线的斜率,求出切线方程,把点
处的切线的斜率,求出切线方程,把点![]() 代入切线方程中,求出
代入切线方程中,求出![]() 的值;
的值;
(Ⅱ) (ⅰ) ![]() ,
,![]() ,
,![]() ,分类讨论函数的单调性;
,分类讨论函数的单调性;
当![]() 时,可以判断函数没有极值,不符合题意;
时,可以判断函数没有极值,不符合题意;
当![]() 时,可以证明出函数有两个极值点
时,可以证明出函数有两个极值点![]() ,
,![]() ,故可以求出
,故可以求出![]() 的取值范围;
的取值范围;
由(ⅰ)知![]() 在
在![]() 上单调递减,
上单调递减,![]() ,且
,且![]() ,
,
由![]() 得
得![]() ,
,![]() ,又
,又![]() ,
,![]()
![]() .
.
法一:先证明![]() (
(![]() )成立,应用这个不等式,利用放缩法可以证明出
)成立,应用这个不等式,利用放缩法可以证明出![]() 成立;
成立;
法二:令![]() (
(![]() ),求导,利用单调性也可以证明出
),求导,利用单调性也可以证明出
![]() 成立.
成立.
解:(Ⅰ)![]() ,
,![]()
又![]()
![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]()
![]() 切线过点
切线过点![]() ,
,![]()
(Ⅱ)(ⅰ) ![]() ,
,![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,![]() 无极值,不合题意,舍去
无极值,不合题意,舍去
当![]() 时,令
时,令![]() ,得
,得![]() ,
,![]() (
(![]() ),
),
![]() 或
或![]() ;
;![]() ,
,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,![]() 恰有个极值点
恰有个极值点![]() ,
,![]() ,符合题意,
,符合题意,
故![]() 的取值范围是
的取值范围是![]()
(ⅱ)由(ⅰ)知![]() 在
在![]() 上单调递减,
上单调递减,![]() ,且
,且![]() ,
,
由![]() 得
得![]() ,
,![]() ,又
,又![]() ,
,![]()
![]()
法一:下面证明![]() (
(![]() ),令
),令![]() (
(![]() ),
),![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,即
,即![]() (
(![]() ),
),
![]() ,
,
综上![]()
法二:令![]() (
(![]() ),则
),则![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,即
,即![]() ,
,
综上![]()


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据报道,某公司的33名职工的月工资(以元为单位)如下:
职务 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 管理员 | 职员 |
人数 | 1 | 1 | 2 | 1 | 5 | 3 | 20 |
工资 | 5500 | 5500 | 3500 | 3000 | 2500 | 2000 | 1500 |
(1)求该公司职工月工资的平均数(精确到元);
(2)假设副董事长的工资从5000元提升到20000元,董事长的工资从5500元提升到30000元,那么新的平均数又是什么?(精确到元)
(3)你认为工资的平均数能反映这个公司员工的工资水平吗?结合此问题谈一谈你的看法.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且满足
上,且满足![]() ,(
,(![]() 为坐标原点).
为坐标原点).
(1)求抛物线![]() 的方程;
的方程;
(2)过点![]() 作斜率乘积为1的两条不重合的直线
作斜率乘积为1的两条不重合的直线![]() ,且
,且![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,线段
两点,线段![]() 的中点分别为
的中点分别为![]() ,求证:直线
,求证:直线![]() 过定点,并求出定点坐标.
过定点,并求出定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】北京、张家口2022年冬奥会申办委员会在俄罗斯索契举办了发布会,某公司为了竞标配套活动的相关代言,决定对旗下的某商品进行一次评估,该商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了抓住申奥契机,扩大该商品的影响力,提高年销售量.公司决定立即对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元.公司拟投入
元.公司拟投入![]() 万作为技改费用,投入50万元作为固定宣传费用,投入
万作为技改费用,投入50万元作为固定宣传费用,投入![]() 万元作为浮动宣传费用.试问:当该商品改革后的销售量
万元作为浮动宣传费用.试问:当该商品改革后的销售量![]() 至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使改革后的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(Ⅰ)求直线![]() 的参数方程和极坐标方程;
的参数方程和极坐标方程;
(Ⅱ)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产
万元,并且每生产![]() 百台的生产成本为
百台的生产成本为![]() 万元(总成本
万元(总成本![]() 固定成本
固定成本![]() 生产成本).销售收入
生产成本).销售收入![]() (万元)满足
(万元)满足![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
(1)写出利润函数![]() 的解析式(利润
的解析式(利润![]() 销售收入
销售收入![]() 总成本);
总成本);
(2)工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为丰富市民的文化生活,市政府计划在一块半径为200m,圆心角为![]() 的扇形地上建造市民广场,规划设计如图:内接梯形
的扇形地上建造市民广场,规划设计如图:内接梯形![]() 区域为运动休闲区,其中A,B分别在半径
区域为运动休闲区,其中A,B分别在半径![]() ,
,![]() 上,C,D在圆弧
上,C,D在圆弧![]() 上,
上,
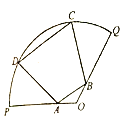
![]() ;上,
;上,![]() ;
;![]() 区域为文化展区,
区域为文化展区,![]() 长为
长为![]() ,其余空地为绿化区域,且
,其余空地为绿化区域,且![]() 长不得超过200m.
长不得超过200m.
(1)试确定A,B的位置,使![]() 的周长最大?
的周长最大?
(2)当![]() 的周长最长时,设
的周长最长时,设![]() ,试将运动休闲区
,试将运动休闲区![]() 的面积S表示为
的面积S表示为![]() 的函数,并求出S的最大值.
的函数,并求出S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com