
°æƒø°ø“—÷™ ˝¡–{an}µƒ∏˜œÓæ˘Œ™’˝ ˝£¨∆‰«∞nœÓµƒ∫ÕŒ™Sn £¨ «“∂‘»Œ“‚µƒm£¨n° N*£¨
∂º”–£®Sm+n+S1£©2=4a2ma2n £Æ
£®1£©«Û ![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©«Û÷§£∫{an}Œ™µ»±» ˝¡–£ª
£®3£©“—÷™ ˝¡–{cn}£¨{dn}¬˙◊„|cn|=|dn|=an £¨ p£®p°ð3£© «∏¯∂®µƒ’˝’˚ ˝£¨ ˝¡–{cn}£¨{dn}µƒ«∞pœÓµƒ∫Õ∑÷±Œ™Tp £¨ Rp £¨ «“Tp=Rp £¨ «Û÷§£∫∂‘»Œ“‚’˝’˚ ˝k£®1°Ðk°Ðp£©£¨ck=dk £Æ
°æ¥∞∏°ø
£®1£©Ω‚£∫”…£®Sm+n+S1£©2=4a2ma2n£Æ»°m=n=1£¨ø…µ√ ![]() £¨
£¨
°þa1£¨a2£æ0£¨°ýa2+2a1=2a2£¨ªØŒ™ ![]() =2
=2
£®2£©÷§√˜£∫”…£®Sm+n+S1£©2=4a2ma2n£Æ
¡Óm=n£¨ø…µ√S2n+a1=2a2n£¨¢Ÿ
°ýS2n+2+a1=2a2n+2£Æ¢⁄
¡Óm=n+1£¨ø…µ√ ![]() £¨¢€
£¨¢€
°ý¢€©Å¢Ÿø…µ√£∫a2n+1=2 ![]() ©Å2a2n=
©Å2a2n= ![]()
![]() £¨¢Ð
£¨¢Ð
¢⁄©Å¢€ø…µ√£∫a2n+2= ![]() £¨¢ð
£¨¢ð
”…¢Ð¢ðø…µ√£∫ ![]() £¨¢Þ
£¨¢Þ
∞—¢Þ¥˙»Î¢Ðø…µ√£∫a2n+1=2a2n£¨
∞—¢Þ¥˙»Î¢ðø…µ√£∫a2n+2=2a2n+1£¨
°ý ![]() =2£¨”÷
=2£¨”÷ ![]() =2£Æ°ý
=2£Æ°ý ![]() £¨n° N*£Æ
£¨n° N*£Æ
°ý{an}Œ™µ»±» ˝¡–£¨ ◊œÓŒ™a1£¨π´±»Œ™2
£®3£©÷§√˜£∫”…£®2£©ø…÷™£∫an= ![]() £¨
£¨
°þ|cn|=|dn|=an= ![]() £¨
£¨
°ýcp=°¿dp£¨»Ùcp=©Ådp£¨
≤ª∑¡…Ëcp£æ0£¨cp£º0£¨
‘ÚTp°ð ![]() ©Å
©Å ![]() =
= ![]() ©Å
©Å ![]() =a1£æ0£¨
=a1£æ0£¨
Rp°Ð©Å ![]() +
+ ![]() =©Å
=©Å ![]() +
+ ![]() =©Åa1£º0£¨
=©Åa1£º0£¨
’‚”ÎTp=Rp√¨∂У¨°ýcp=dp£¨
”⁄ «Tp©Å1=Rp©Å1£¨ø…µ√cp©Å1=dp©Å1£¨”⁄ «cp©Å2=dp©Å2£¨°≠£¨c1=d1£Æ
°ý∂‘»Œ“‚’˝’˚ ˝k£®1°Ðk°Ðp£©£¨ck=dk£Æ
°æΩ‚Œˆ°ø£®1£©”…£®Sm+n+S1£©2=4a2ma2n £Æ »°m=n=1£¨ø…µ√ ![]() £¨¿˚”√a1 £¨ a2£æ0£¨º¥ø…µ√≥ˆ£Æ£®2£©”…£®Sm+n+S1£©2=4a2ma2n £Æ ¡Óm=n£¨ø…µ√S2n+a1=2a2n £¨ S2n+2+a1=2a2n+2 £Æ ¡Óm=n+1£¨ø…µ√
£¨¿˚”√a1 £¨ a2£æ0£¨º¥ø…µ√≥ˆ£Æ£®2£©”…£®Sm+n+S1£©2=4a2ma2n £Æ ¡Óm=n£¨ø…µ√S2n+a1=2a2n £¨ S2n+2+a1=2a2n+2 £Æ ¡Óm=n+1£¨ø…µ√ ![]() £¨ªØºÚ’˚¿Ìø…µ√£∫a2n+1=2a2n £¨ a2n+2=2a2n+1 £¨ ¿˚”√µ»±» ˝¡–µƒÕ®œÓπ´ Ωº¥ø…µ√≥ˆ£Æ£®3£©”…£®2£©ø…÷™£∫an=
£¨ªØºÚ’˚¿Ìø…µ√£∫a2n+1=2a2n £¨ a2n+2=2a2n+1 £¨ ¿˚”√µ»±» ˝¡–µƒÕ®œÓπ´ Ωº¥ø…µ√≥ˆ£Æ£®3£©”…£®2£©ø…÷™£∫an= ![]() £¨”…”⁄|cn|=|dn|=an=
£¨”…”⁄|cn|=|dn|=an= ![]() £¨ø…µ√cp=°¿dp £¨ »Ùcp=©Ådp £¨ ≤ª∑¡…Ëcp£æ0£¨cp£º0£¨‘ÚTp°ða1£æ0£¨Rp°Ð©Åa1£º0£¨’‚”ÎTp=Rp√¨∂У¨ø…µ√cp=dp £¨ ”⁄ «Tp©Å1=Rp©Å1 £¨ º¥ø…÷§√˜£Æ
£¨ø…µ√cp=°¿dp £¨ »Ùcp=©Ådp £¨ ≤ª∑¡…Ëcp£æ0£¨cp£º0£¨‘ÚTp°ða1£æ0£¨Rp°Ð©Åa1£º0£¨’‚”ÎTp=Rp√¨∂У¨ø…µ√cp=dp £¨ ”⁄ «Tp©Å1=Rp©Å1 £¨ º¥ø…÷§√˜£Æ
°æøºµ„æ´Œˆ°øÕ®π˝¡ÈªÓ‘À”√ ˝¡–µƒ«∞nœÓ∫Õ∫Õ ˝¡–µƒÕ®œÓπ´ Ω£¨’∆Œ’ ˝¡–{an}µƒ«∞nœÓ∫Õsn”ÎÕ®œÓanµƒπÿœµ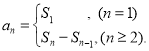 £ª»Áπ˚ ˝¡–anµƒµ⁄nœÓ”În÷ƺ‰µƒπÿœµø…“‘”√“ª∏ˆπ´ Ω±Ì æ£¨ƒ«√¥’‚∏ˆπ´ ΩæÕΩ–’‚∏ˆ ˝¡–µƒÕ®œÓπ´ Ωº¥ø…“‘Ω‚¥¥À£Æ
£ª»Áπ˚ ˝¡–anµƒµ⁄nœÓ”În÷ƺ‰µƒπÿœµø…“‘”√“ª∏ˆπ´ Ω±Ì æ£¨ƒ«√¥’‚∏ˆπ´ ΩæÕΩ–’‚∏ˆ ˝¡–µƒÕ®œÓπ´ Ωº¥ø…“‘Ω‚¥¥À£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËOŒ™◊¯±Í‘≠µ„£¨«˙œþx2+y2+2x©Å6y+1=0…œ”–¡Ωµ„P°¢Q£¨¬˙◊„πÿ”⁄÷±œþx+my+4=0∂‘≥∆£¨”÷¬˙◊„ ![]() =0£Æ
=0£Æ
£®1£©«Ûmµƒ÷µ£ª
£®2£©«Û÷±œþPQµƒ∑Ω≥ãÆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨“—÷™œþ∂ŒAB≥§∂»Œ™a£®aŒ™∂®÷µ£©£¨‘⁄∆‰…œ»Œ“‚—°»°“ªµ„M£¨‘⁄ABµƒÕ¨“ª≤ý∑÷±“‘AM°¢MBŒ™µ◊◊˜’˝∑Ω–ŒAMCD°¢MBEF£¨°—P∫Õ°—Q «’‚¡Ω∏ˆ’˝∑Ω–ŒµƒÕ‚Ω”‘≤£¨À¸√«Ωª”⁄µ„M°¢N£Æ ‘“‘AŒ™◊¯±Í‘≠µ„£¨Ω®¡¢ µ±µƒ∆Ω√Ê÷±Ω«◊¯±Íœµ£Æ 
£®1£©÷§√˜£∫≤ª¬€µ„M»Á∫Œ—°»°£¨÷±œþMN∂ºÕ®π˝“ª∂®µ„S£ª
£®2£©µ± ![]() ±£¨π˝A◊˜°—Qµƒ∏Óœþ£¨Ωª°—Q”⁄G°¢H¡Ωµ„£¨‘⁄œþ∂ŒGH…œ»°“ªµ„K£¨ π
±£¨π˝A◊˜°—Qµƒ∏Óœþ£¨Ωª°—Q”⁄G°¢H¡Ωµ„£¨‘⁄œþ∂ŒGH…œ»°“ªµ„K£¨ π ![]() =
= ![]() «Ûµ„KµƒπϺ££Æ
«Ûµ„KµƒπϺ££Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∏˜œÓæ˘¥Û”⁄1µƒ ˝¡–{an}¬˙◊„£∫a1= ![]() £¨an+1=
£¨an+1= ![]() £®an+
£®an+ ![]() £©£¨£®n° N*£©£¨bn=log5
£©£¨£®n° N*£©£¨bn=log5 ![]() £Æ
£Æ
£®1£©÷§√˜{bn}Œ™µ»±» ˝¡–£¨≤¢«Û{bn}Õ®œÓπ´ Ω£ª
£®2£©»Ùcn= ![]() £¨TnŒ™{cn}µƒ«∞nœÓ∫Õ£¨«Û÷§£∫Tn£º6£Æ
£¨TnŒ™{cn}µƒ«∞nœÓ∫Õ£¨«Û÷§£∫Tn£º6£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“‘œ¬»˝∏ˆπÿ”⁄‘≤◊∂«˙œþµƒ√¸Ã‚÷–£∫
¢Ÿ…ËA£¨BŒ™¡Ω∏ˆ∂®µ„£¨KŒ™∑«¡„≥£ ˝£¨»Ù|PA|©Å|PB|=K£¨‘Ú∂ص„PµƒπϺ£ «À´«˙œþ£Æ
¢⁄∑Ω≥Ã2x2©Å5x+2=0µƒ¡Ω∏˘ø…∑÷±◊˜Œ™Õ÷‘≤∫ÕÀ´«˙œþµƒ¿Î–ƒ¬
¢€À´«˙œþ ![]() ”ÎÕ÷‘≤
”ÎÕ÷‘≤ ![]() +y2=1”–œýÕ¨µƒΩ𵄣Æ
+y2=1”–œýÕ¨µƒΩ𵄣Æ
¢Ð“—÷™≈◊ŒÔœþy2=2px£¨“‘π˝Ω𵄵ƒ“ªÃıœ“ABŒ™÷±æ∂◊˜‘≤£¨‘Ú¥À‘≤”Î◊ºœþœý«–
∆‰÷–’Ê√¸Ã‚Œ™£®–¥≥ˆÀ˘“‘’Ê√¸Ã‚µƒ–Ú∫≈£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…ËÀ´«˙œþ ![]() µƒ¿Î–ƒ¬ e=2£¨”“Ωπµ„Œ™F£®c£¨0£©£¨∑Ω≥Ãax2+bx©Åc=0µƒ¡Ω∏ˆ µ∏˘∑÷±Œ™x1∫Õx2 £¨ ‘Úµ„P£®x1 £¨ x2£© ¬˙◊„£® £©
µƒ¿Î–ƒ¬ e=2£¨”“Ωπµ„Œ™F£®c£¨0£©£¨∑Ω≥Ãax2+bx©Åc=0µƒ¡Ω∏ˆ µ∏˘∑÷±Œ™x1∫Õx2 £¨ ‘Úµ„P£®x1 £¨ x2£© ¬˙◊„£® £©
A.±ÿ‘⁄‘≤x2+y2=2ƒ⁄
B.±ÿ‘⁄‘≤x2+y2=2Õ‚
C.±ÿ‘⁄‘≤x2+y2=2…œ
D.“‘…œ»˝÷÷«È–Œ∂º”–ø…ƒÐ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™≈◊ŒÔœþ![]() µƒΩπµ„Œ™
µƒΩπµ„Œ™![]() £¨«„–±Ω«Œ™
£¨«„–±Ω«Œ™![]() µƒ÷±œþ
µƒ÷±œþ![]() π˝µ„
π˝µ„![]() ”ÎíŌԜþ
”ÎíŌԜþ![]() Ωª”⁄
Ωª”⁄![]() ¡Ωµ„£¨
¡Ωµ„£¨ ![]() Œ™◊¯±Í‘≠µ„£¨
Œ™◊¯±Í‘≠µ„£¨ ![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() .
.
£®1£©«Û![]() £ª
£ª
£®2£©…˵„![]() Œ™÷±œþ
Œ™÷±œþ![]() ”ÎíŌԜþ
”ÎíŌԜþ![]() ‘⁄µ⁄“ªœÛœÞµƒΩªµ„£¨π˝µ„
‘⁄µ⁄“ªœÛœÞµƒΩªµ„£¨π˝µ„![]() ◊˜
◊˜![]() µƒ–±¬ ∑÷±Œ™
µƒ–±¬ ∑÷±Œ™![]() µƒ¡ΩÃıœ“
µƒ¡ΩÃıœ“![]() £¨»Áπ˚
£¨»Áπ˚![]() £¨÷§√˜÷±œþ
£¨÷§√˜÷±œþ![]() π˝∂®µ„£¨≤¢«Û≥ˆ∂®µ„◊¯±Í.
π˝∂®µ„£¨≤¢«Û≥ˆ∂®µ„◊¯±Í.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø…˜ڡø ![]() =£®
=£® ![]() sinx£¨sinx£©£¨
sinx£¨sinx£©£¨ ![]() =£®cosx£¨sinx£©£¨x° [0£¨
=£®cosx£¨sinx£©£¨x° [0£¨ ![]() ]
]
£®1£©»Ù| ![]() |=|
|=| ![]() |£¨«Ûxµƒ÷µ£ª
|£¨«Ûxµƒ÷µ£ª
£®2£©…Ë∫Ø ˝f£®x£©= ![]()
![]() £¨«Ûf£®x£©µƒ÷µ”Ú£Æ
£¨«Ûf£®x£©µƒ÷µ”Ú£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥÷–—ßµ˜≤È¡Àƒ≥∞ý»´≤ø45√˚Õ¨—ß≤Œº” È∑®…ÁÕ≈∫Õ—ðΩ≤…ÁÕ≈µƒ«Èøˆ£¨ ˝æð»Áœ¬±Ì£∫£®µ•Œª£∫»À£©
≤Œº” È∑®…ÁÕ≈ | Œ¥≤Œº” È∑®…ÁÕ≈ | |
≤Œº”—ðΩ≤…ÁÕ≈ | 8 | 5 |
Œ¥≤Œº”—ðΩ≤…ÁÕ≈ | 2 | 30 |
£®1£©¥”∏√∞ýÀʪ˙—°1√˚Õ¨—ߣ¨«Û∏√Õ¨—ß÷¡…Ÿ≤Œº”“ª∏ˆ…ÁÕ≈µƒ∏≈¬ £ª
£®2£©‘⁄º»≤Œº” È∑®…ÁÕ≈”÷≤Œº”—ðΩ≤…ÁÕ≈µƒ8√˚Õ¨—ß÷–£¨”–5√˚ƒ–Õ¨—ßA1 £¨ A2 £¨ A3 £¨ A4 £¨ A5 £¨ 3√˚≈ÆÕ¨—ßB1 £¨ B2 £¨ B3 £Æ œ÷¥”’‚5√˚ƒ–Õ¨—ß∫Õ3√˚≈ÆÕ¨—ß÷–∏˜Àʪ˙—°1»À£¨«ÛA1±ª—°÷–«“B1Œ¥±ª—°÷–µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com