Question

已知函数f(x)=x-

1

x

．
（1）研究此函数的奇偶性．
（2）证明f（x）在（0，+∞）上为增函数．
（3）画出此函数的图象草图．

Answer 1

分析：（1）先求得f（x）的定义域关于原点对称，且对定义域内任意x，都有f（-x）=-f（x），可得f（x）为奇函数．
（2）任取x₁，x₂∈（0，+∞）且x₁＜x₂，计算f(x1)-f(x2)=(x1-

1

x1

)-(x2-

1

x2

)=＜0，可得f（x）在（0，+∞）上为增函数．
（3）由（1）知，f（x）的图象关于原点对称，先用描点法画出f（x）在（0，+∞）的图象，再将所得图象关于原点对称得到f（x）在（-∞，0）内的图象．

解答：解：（1）f（x）的定义域为（-∞，0）∪（0，+∞）且对定义域内任意x，都有f(-x)=(-x)-

1

-x

=-(x-

1

x

)=-f(x)，
∴f（x）为奇函数．
（2）任取x₁，x₂∈（0，+∞）且x₁＜x₂，则x₁-x₂＜0，x₁x₂＞0，∴1+

1

x1x2

＞0．
计算f(x1)-f(x2)=(x1-

1

x1

)-(x2-

1

x2

)=(x1-x2)+(

1

x2

-

1

x1

)=(x1-x2)•(1+

1

x1x2

)＜0，
∴f（x₁）＜f（x₂），由增函数定义可知，f（x）在（0，+∞）上为增函数．
（3）由（1）知，f（x）的图象关于原点对称，先画出f（x）在（0，+∞）的图象，再将所得图象关于原点对称得到f（x）在（-∞，0）内的图象；由（2）知f（x）在（0，+∞）上递增，
列表：

x	…	1 4	1 2	1	2	4	…
f（x）	…	- 15 4	- 3 2	0	3 2	15 4	…

画出草图如下：
．

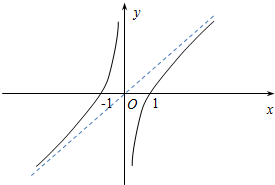
点评：本题主要考查函数的单调性、奇偶性的判断和证明，用描点法作函数的图象，属于中档题．