解:(I)由题设知
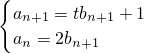
,得
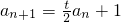
.
又已知t≠2,可得
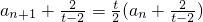
.
由t≠0,t≠2,f(b)≠g(b),可知
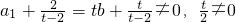
,
所以
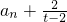
是等比数列,其首项为
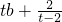
,公比为

.
于是
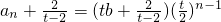
,即
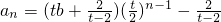
.
又
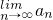
存在,可得
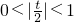
,所以-2<t<2且t≠0.
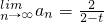
.
(II)证明:因为g(x)=f
-1(x),
所以a
n=g(b
n+1)=f
-1(b
n+1),即b
n+1=f(a
n).
下面用数学归纳法证明a
n+1<a
n(n∈N
*).
(1)当n=1(2)时,由f(x)(3)为增函数,且f(1)<1(4),
得a
1=f(b
1)=f(1)<1(5),b
2=f(a
1)<f(1)<1(6),a
2=f(b
2)<f(1)=a
1(7),
即a
2<a
1,结论成立.
(8)假设n=k(9)时结论成立,即a
k+1<a
k(10).由f(x)(11)为增函数,得f(a
k+1)<f(a
k)(12),即b
k+2<b
k+1(13),进而得f(b
k+2)<f(b
k+1)(14),即a
k+2<a
k+1(15),这就是说当n=k+1(16)时,结论也成立.根据(1)和(2)可知,对任意的n∈N
*(17),a
n+1<a
n(18).
分析:(I)由题设知
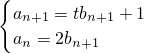
,所以
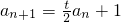
.由t≠2,知
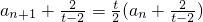
.由t≠0,t≠2,
f(b)≠g(b),知
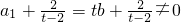
,
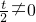
,分析可得答案.
(II)因为g(x)=f
-1(x),所以b
n+1=f(a
n).然后用数学归纳法证明a
n+1<a
n(n∈N
*).
点评:本题考查数列的性质和应用,解题时要注意公式的合理运用.

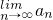 存在,求x的取值范围;
存在,求x的取值范围;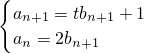 ,得
,得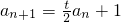 .
.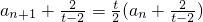 .
.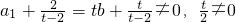 ,
,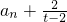 是等比数列,其首项为
是等比数列,其首项为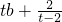 ,公比为
,公比为 .
.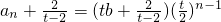 ,即
,即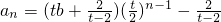 .
.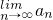 存在,可得
存在,可得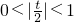 ,所以-2<t<2且t≠0.
,所以-2<t<2且t≠0.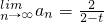 .
.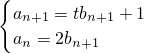 ,所以
,所以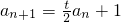 .由t≠2,知
.由t≠2,知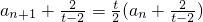 .由t≠0,t≠2,
.由t≠0,t≠2,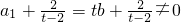 ,
,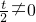 ,分析可得答案.
,分析可得答案.
