
【题目】已知![]() 为奇函数,
为奇函数,![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)如函数![]() 在区间
在区间![]() 上为单调函数,求实数
上为单调函数,求实数![]() 的范围.
的范围.
(3)若关于![]() 的方程
的方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】试题
(1)依题意,由![]() ,即可求得
,即可求得![]() 及
及![]() 解析式;(2)因为
解析式;(2)因为![]() ,所以
,所以![]() ,由二次函数的性质可知,要使函数
,由二次函数的性质可知,要使函数![]() 在区间
在区间![]() 上为单调函数,,只要
上为单调函数,,只要![]() 或
或![]() 即可,由此即可求出结果;(3)因为
即可,由此即可求出结果;(3)因为![]() ,所以
,所以![]() ,然后再进行换元,令
,然后再进行换元,令![]() , 因为
, 因为![]() 的定义域为
的定义域为![]() ,
,![]() ,可得
,可得![]() ,则
,则![]() ,由于关于
,由于关于![]() 的方程
的方程![]() 有解,则
有解,则![]() ,由此即可求出结果.
,由此即可求出结果.
试题解析:(1)因为![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,
所以![]() ,
,![]() ,
,
![]() ,①
,①
![]() 令
令![]() 取
取![]() 代入上式得
代入上式得![]() ,
,
即![]() ,②
,②
联立①②可得,![]() ,
,
![]() .
.
(2)因为![]() ,
,
所以![]() ,
,
因为函数![]() 在区间
在区间![]() 上为单调函数,
上为单调函数,
所以![]() 或
或![]() ,
,
所以所求实数![]() 的取值范围为:
的取值范围为:![]() 或
或![]() .
.
(3)因为![]() ,
,
所以![]() ,
,
设![]() ,
,
则![]() ,
,
因为![]() 的定义域为
的定义域为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即![]() ,则
,则![]() ,
,
因为关于![]() 的方程
的方程![]() 有解,则
有解,则![]() ,
,
故![]() 的取值范围为
的取值范围为 ![]() .
.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实数,
为实数,![]() ,
,![]() ).
).
(1)当函数![]() 的图象过点
的图象过点![]() ,且方程
,且方程![]() 有且只有一个根,求
有且只有一个根,求![]() 的表达式;
的表达式;
(2)在(1)的条件下,当![]() 时,
时,![]() 是单调函数,求实数
是单调函数,求实数![]() 的取值范围;
的取值范围;
(3)若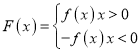 ,当
,当![]() ,
,![]() ,
,![]() ,且函数
,且函数![]() 为偶函数时,试判断
为偶函数时,试判断![]() 能否大于
能否大于![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,若存在闭区间
,若存在闭区间![]() ,使得函数
,使得函数![]() 满足:①
满足:①![]() 在
在![]()
上是单调函数;②![]() 在
在 ![]() 上的值域是
上的值域是![]() ,则称区间
,则称区间![]() 是函数
是函数 ![]() 的“和谐区间”,
的“和谐区间”,
下列结论错误的是( )
A.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
B.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
C.函数 ![]() 不存在 “和谐区间”
不存在 “和谐区间”
D.函数 ![]() 存在 “和谐区间”
存在 “和谐区间”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某湿地公园内有一条河,现打算建一座桥将河两岸的路连接起来,剖面设计图纸如下:

其中,点![]() 为
为![]() 轴上关于原点对称的两点,曲线段
轴上关于原点对称的两点,曲线段![]() 是桥的主体,
是桥的主体,![]() 为桥顶,且曲线段
为桥顶,且曲线段![]() 在图纸上的图形对应函数的解析式为
在图纸上的图形对应函数的解析式为![]() ,曲线段
,曲线段![]() 均为开口向上的抛物线段,且
均为开口向上的抛物线段,且![]() 分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(
分别为两抛物线的顶点,设计时要求:保持两曲线在各衔接处(![]() )的切线的斜率相等.
)的切线的斜率相等.
(1)求曲线段![]() 在图纸上对应函数的解析式,并写出定义域;
在图纸上对应函数的解析式,并写出定义域;
(2)车辆从![]() 经
经![]() 倒
倒![]() 爬坡,定义车辆上桥过程中某点
爬坡,定义车辆上桥过程中某点![]() 所需要的爬坡能力为:
所需要的爬坡能力为:![]() (该点
(该点![]() 与桥顶间的水平距离)
与桥顶间的水平距离)![]() (设计图纸上该点处的切线的斜率),其中
(设计图纸上该点处的切线的斜率),其中![]() 的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为
的单位:米.若该景区可提供三种类型的观光车:①游客踏乘;②蓄电池动力;③内燃机动力.它们的爬坡能力分别为![]() 米,
米,![]() 米,
米,![]() 米,又已知图纸上一个单位长度表示实际长度
米,又已知图纸上一个单位长度表示实际长度![]() 米,试问三种类型的观光车是否都可以顺利过桥?
米,试问三种类型的观光车是否都可以顺利过桥?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量按照其质量指标值M进行等级划分,具体如下表:
质量指标值M |
|
|
|
等级 | 三等品 | 二等品 | 一等品 |
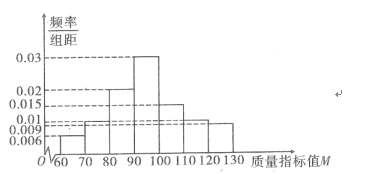
现从某企业生产的这种产品中随机抽取了100件作为样本,对其质量指标值M进行统计分析,得到如图所示的频率分布直方图.
(1)记A表示事件“一件这种产品为二等品或一等品”,试估计事件A的概率;
(2)已知该企业的这种产品每件一等品、二等品、三等品的利润分别为10元、6元、2元,试估计该企业销售10000件该产品的利润;
(3)根据该产品质量指标值M的频率分布直方图,求质量指标值M的中位数的估计值(精确到0.01)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)是否存在实数![]() ,使得
,使得![]() 与
与![]() 的单调区间相同,若存在,求出
的单调区间相同,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若![]() ,求证:
,求证:![]() 在
在![]() 上恒成立.
上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.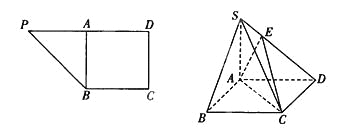
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com