练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．在△ABC中，已知A=30°，B=120°，b=5，解三角形．

    分析 由三角形的内角和可得C，可得等腰三角形，由正弦定理可得a和c．

    解答 解：∵A=30°，B=120°，∴C=180°-（A+B）=30°．
    ∴A=C，∴a=c．由正弦定理可得a=$\frac{bsinA}{sinB}$=$\frac{5sin30°}{sin120°}$=$\frac{5\sqrt{3}}{3}$，
    综上可知，C=30°，a=c=$\frac{5\sqrt{3}}{3}$

    点评 本题考查解三角形，涉及正余弦定理的应用，属基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．函数y=ln（ax2+x-1）的值域为R，当且仅当（　　）
    A．a≥0B．a＞0C．a$≥-\frac{1}{4}$D．a$＜-\frac{1}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．给出如下说法：
    ①命题“若x2-3x+2=0，则x=1”的逆否命题是“若x≠1，则x2-3x+2≠0”
    ②若命题p：?x∈R，x2+x+1=0，则￢p：?x∈R，x2+x+1≠0
    ③若p∧q为假命题，则p，q均为假命题
    ④“x＞2”是“x2-3x+2＞0”的充分不必要条件
    其中正确命题的序号有①②④．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．（1）若6x=24y=12，求$\frac{1}{x}$+$\frac{1}{y}$的值；
    （2）解方程：1og2（2x+8）=x+1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知a＞0，函数f（x）=eaxsinx（x∈[0，+∞））．记xn为f（x）的从小到大的第n（n∈N*）个极值点，则数列{f（xn）}是（　　）
    A．等差数列，公差为eaxB．等差数列，公差为-eax
    C．等比数列，公比为eaxD．等比数列，公比为-eax

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．某高三年级从甲（文）乙（理）两个年级组各选出7名学生参加高校自主招生数学选拔考试，他们取得的成绩（满分：100分）的茎叶图如图所示，其中甲组学生的平均分是85分，乙组学生成绩的中位数是83分．
    （1）求x和y的值；
    （2）从成绩在90分以上的学生中随机取两名学生，求甲组至少有一名学生的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．设数列{an}满足a1=1，an+1=3an．
    （1）求{an}的通项公式及前n项和Sn；
    （2）已知{bn}是等差数列，Tn为前n项和，且b1=a2，b2=a1+a2+a3，求T38．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

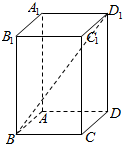    16．如图，在正四棱柱中ABCD-A1B1C1D1，AB=1，D1B和平面ABCD所成的角的大小为$arctan\frac{{3\sqrt{2}}}{4}$，求该四棱柱的表面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

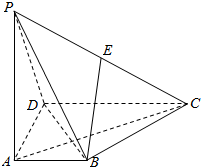    17．如图，在四棱锥P-ABCD中，PA⊥ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，点E为棱PC的中点．
    （1）证明BE⊥DC；
    （2）求二面角E-AB-P的值；
    （3）求直线BE与平面PBD所成角的正弦值．

    查看答案和解析>>

    同步练习册答案