
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
分析 利用条件以及诱导公式,求得要求式子的值.
解答 解:∵f(x-π)=f(x)+sinx,当0≤x≤π,f(x)=1时,
则$f({-\frac{13π}{6}})$=f(-$\frac{7π}{6}$-π)=f(-$\frac{7π}{6}$)+sin(-$\frac{7π}{6}$)=f(-$\frac{π}{6}$-π)+sin(-$\frac{7π}{6}$)
=f(-$\frac{π}{6}$)+sin(-$\frac{π}{6}$)+sin(-$\frac{7π}{6}$)=f($\frac{5π}{6}$-π)+sin(-$\frac{π}{6}$)-sin$\frac{7π}{6}$
=f($\frac{5π}{6}$)+sin$\frac{5π}{6}$+sin(-$\frac{π}{6}$)+sin$\frac{π}{6}$=1+$\frac{1}{2}$-$\frac{1}{2}$+$\frac{1}{2}$=$\frac{3}{2}$,
故选:C.
点评 本题主要考查新定义,诱导公式的应用,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
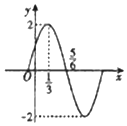
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (4,+∞) | C. | (0,4) | D. | (-∞,0)∪(4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示.将日销售量落入各组的频率视为概率,并假设每天的销售量相互独立.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com