已知
．求证:
．
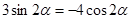证明过程见试题解析．
解析试题分析：本题属于三角恒等式的证明，三角恒等式的证明方法灵活多样，可总结如下：（1）从一边开始直接推证等于另一边，一般地，如果所证等式一边比较复杂而另一边比较简单时多采用此法，即由繁到简；（2）左右归一法，即将所证恒等式左，右两边同时推导变形，直接推得左右两边都等于同一个式子；（2）比较法，即设法证明“左边-右边=0”，或“左边/右边=1”；（4）分析法，从被证的等式出发，逐步地探求使等式成立的充分条件，一直到已知条件或显然成立的结论为止，就可以判断原等式成立．本题适用于第四类，观察发现条件中所给角为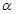
，结论中所给角为
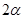，可将所证等式利用倍角公式展开，可化为
又由条件将正切化为正余弦可得
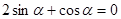．等式成立．
解：因为，所以1+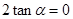
，
从而,,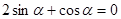
另一方面：要证,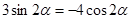
只要证：
,
即证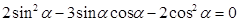 
,
即证 ,
由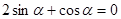可得成立,
于是命题得证．
考点：三角恒等变形．
阅读快车系列答案科目：高中数学 来源： 题型：解答题
已知函数f(x)＝cos(
＋x)·cos(－x)，g(x)＝
sin2x－
．
(1)求函数f(x)的最小正周期；
(2)求函数h(x)＝f(x)－g(x)的最大值，并求使h(x)取得最大值的x的集合．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，半圆O的直径为2，A为直径延长线上的一点，OA＝2，B为半圆上任意一点，以AB为一边作等边三角形ABC.问：点B在什么位置时，四边形OACB面积最大？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
中，
，三角形面积为
，则
的值为 . 
=（cos
，sin
=（cos
，sin
｜＝
．
＜
，－
，求sin
．
的最小正周期；
，且
，求
．
分别为△ABC三个内角A、B、C的对边，
.
，△ABC 的面积为
，求
.
的值；
，
，
，
，求
的值．
，且
．
的值； （2）求
的值．